
【题目】如图,已知矩形ABCD的四个顶点都在双曲线y=![]() (k>0)上,BC=2AB,且矩形ABCD的面积是32,则k的值是( )
(k>0)上,BC=2AB,且矩形ABCD的面积是32,则k的值是( )
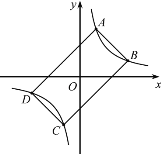
A.6B.8C.10D.12
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
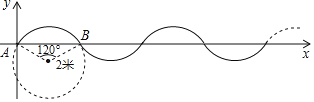
【题目】如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°圆弧多次复制并首尾连接而成,现有一点P从A(A为坐标原点),以每秒![]() 米的速度沿曲线向右运动,则在第2020秒时点P的纵坐标为_____.
米的速度沿曲线向右运动,则在第2020秒时点P的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥百大集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,才能使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
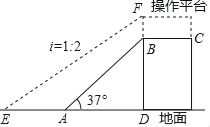
【题目】如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.
(1)求传送带AB的长度;
(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.41,
≈1.41, ![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成不完整的条形统计图和扇形统计图.
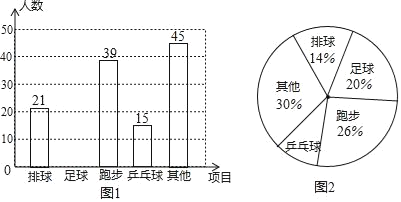
结合以上信息解答下列问题:
(1)m= .
(2)请补全上面的条形统计图;
(3)在图2中,乒乓球所对应扇形的圆心角= ;
(4)已知该校共有2100名学生,请你估计该校约有多少名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AC平分∠DAB,直线DC与AB的延长线相交于点P,AD与PC延长线垂直,垂足为D,CE平分∠ACB,交⊙O于E.
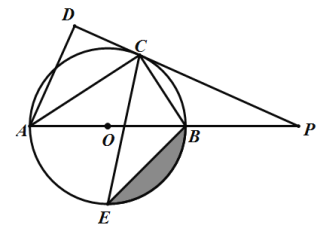
(1)求证:PC与⊙O相切;
(2)若AC=6,tan∠BEC=![]() ,求BE的长度以及图中阴影部分面积.
,求BE的长度以及图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
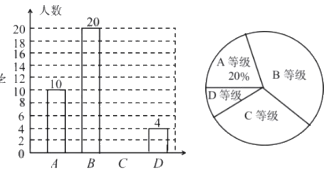
【题目】哈市某中学为了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果外为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若九年级共有600名学生,请你估计九年级学生中体能测试结果为D等级的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
类比定义:我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则等等.小学里,把分子比分母小的分数叫做真分数,类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.
拓展定义:
对于任何一个分式都可以化成整式与真分式的和的形式,
如:![]() ;
;
![]() .
.
理解定义:
(1)下列分式中,属于真分式的是:____属于假分式的是:_____(填序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
拓展应用:
(2)将分式![]() 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;
(3)将假分式![]() 化成整式与真分式的和的形式。
化成整式与真分式的和的形式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com