
°æƒø°øƒ≥–£Œ™¡ÀΩ‚—ß…˙∂‘÷–π˙√Ò◊¿÷∆˜µƒœ≤∞Æ«Èøˆ£¨Àʪ˙≥È»°¡À±æ–£µƒ≤ø∑÷—ß…˙Ω¯––µ˜≤È£®√ø√˚—ß…˙—°‘Ò≤¢«“÷ªƒÐ—°‘Ò“ª÷÷œ≤∞Æ¿÷∆˜£©£¨œ÷Ω´ ’ºØµΩµƒ ˝æðªÊ÷∆»Áœ¬µƒ¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº.
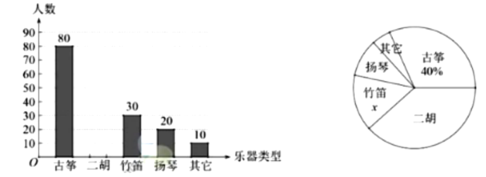
£®1£©’‚¥Œπ≤≥È»° —ß…˙Ω¯––µ˜≤È£¨…»–ŒÕ≥º∆Õº÷–µƒ![]() .
.
£®2£©«Î≤π»´Õ≥º∆Õº£ª
£®3£©‘⁄…»–ŒÕ≥º∆Õº÷–°∞—Ô«Ÿ°±À˘∂‘…»–Œµƒ‘≤–ƒΩ« « ∂»£ª
£®4£©»Ù∏√–£”–3000√˚—ß…˙£¨«Îƒ„π¿º∆∏√–£œ≤∞Æ°∞∂˛∫˙°±µƒ—ß…˙‘º”– √˚.
°æ¥∞∏°ø£®1£©200£¨15%£ª£®2£©Õ≥º∆Õº»ÁÕºÀ˘ æº˚Ω‚Œˆ£ª£®3£©36£ª£®4£©900.
°æΩ‚Œˆ°ø
£®1£©”√œ≤∞Æπ≈Û𵃻À ˝≥˝“‘À˘’º∞Ÿ∑÷±»º¥ø…µ√µΩ≥È≤ȵƒ◊лÀ ˝£¨”√œ≤∞Æ÷Òµ—µƒ»À ˝≥˝“‘◊лÀ ˝º¥ø…µ√≥ˆxµƒ÷µ£ª
£®2£©«Ûµ√œ≤∞Æ∂˛∫˙µƒ»À ˝£¨º¥ø…Ω´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®3£©«Û≥ˆ—Ô«Ÿ≤ø∑÷µƒ∞Ÿ∑÷±»£¨º¥ø…µ√µΩ—Ô«Ÿ≤ø∑÷À˘’º‘≤–ƒΩ«µƒ∂» ˝£ª
£®4£©“¿æðœ≤∞Æ∂˛∫˙µƒ—ß…˙À˘’ºµƒ∞Ÿ∑÷±»£¨º¥ø…µ√µΩ∏√–£œ≤∞Æ∂˛∫˙µƒ—ß…˙ ˝¡ø£Æ
£®1£©80°¬40%=200£®»À£©£¨
x=30°¬200=15%.
£®2£©œ≤∞Æ∂˛∫˙µƒ»À ˝Œ™£∫200-80-30-20-10=60£®»À£©
≤π»´Õº–Œ»Áœ¬£∫

£®3£©°∞—Ô«Ÿ°±À˘∂‘…»–Œµƒ‘≤–ƒΩ«µƒ∂» ˝Œ™£∫![]() .
.
£®4£©3000°¡![]() =900£®»À£©£¨
=900£®»À£©£¨
𠣨»Ù∏√–£”–3000√˚—ß…˙£¨«Îƒ„π¿º∆∏√–£œ≤∞Æ°∞∂˛∫˙°±µƒ—ß…˙‘º”–900√˚.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™°œAOB£Ω60°„£¨∞Îæ∂Œ™2![]() µƒ°—M”αþOA°¢OBœý«–£¨»ÙΩ´°—MÀÆ∆ΩœÚ◊Û∆Ω“∆£¨µ±°—M”αþOAœýΩª ±£¨…ËΩªµ„Œ™E∫ÕF£¨«“EF£Ω6£¨‘Ú∆Ω“∆µƒæý¿ÎŒ™____£Æ
µƒ°—M”αþOA°¢OBœý«–£¨»ÙΩ´°—MÀÆ∆ΩœÚ◊Û∆Ω“∆£¨µ±°—M”αþOAœýΩª ±£¨…ËΩªµ„Œ™E∫ÕF£¨«“EF£Ω6£¨‘Ú∆Ω“∆µƒæý¿ÎŒ™____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
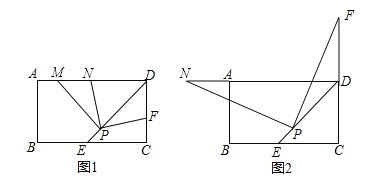
°æƒø°øæÿ–ŒABCD÷–£¨DE∆Ω∑÷°œADCΩªBC±þ”⁄µ„E£¨PŒ™DE…œµƒ“ªµ„£®PE£ºPD£©£¨PM°ÕPD£¨PMΩªAD±þ”⁄µ„M£Æ
£®1£©»Ùµ„F «±þCD…œ“ªµ„£¨¬˙◊„PF°ÕPN£¨«“µ„NŒª”⁄AD±þ…œ£¨»ÁÕº1À˘ æ£Æ
«Û÷§£∫¢ŸPN=PF£ª¢⁄DF+DN=![]() DP£ª
DP£ª
£®2£©»ÁÕº2À˘ 棨µ±µ„F‘⁄CD±þµƒ—”≥§œþ…œ ±£¨»‘»ª¬˙◊„PF°ÕPN£¨¥À ±µ„NŒª”⁄DA±þµƒ—”≥§œþ…œ£¨»ÁÕº2À˘ 棪 ‘Œ DF£¨DN£¨DP”–‘ı—˘µƒ ˝¡øπÿœµ£¨≤¢º”“‘÷§√˜£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¡˙œ∫øÒª∂ºæ‘Ÿ∂»ø™∆Ù£¨µ⁄![]() ΩÏ÷–π˙∫œ∑ ¡˙œ∫Ω⁄µƒ÷˜Ã‚ «°∞»√ƒ„÷™œ∫£¨“≤÷™µæ°±£¨µæÃÔ–°¡˙œ∫—¯÷≥ºº ı‘⁄∫œ∑ ÷бþµƒœÁ’Ú¥Û¡¶Õ∆π„£¨“—÷™√ø«ßøÀ–°¡˙œ∫—¯÷≥≥…±æŒ™
ΩÏ÷–π˙∫œ∑ ¡˙œ∫Ω⁄µƒ÷˜Ã‚ «°∞»√ƒ„÷™œ∫£¨“≤÷™µæ°±£¨µæÃÔ–°¡˙œ∫—¯÷≥ºº ı‘⁄∫œ∑ ÷бþµƒœÁ’Ú¥Û¡¶Õ∆π„£¨“—÷™√ø«ßøÀ–°¡˙œ∫—¯÷≥≥…±æŒ™![]() ‘™£¨‘⁄’˚∏ˆœ˙ €Õ˙ºæµƒ
‘™£¨‘⁄’˚∏ˆœ˙ €Õ˙ºæµƒ![]() ÃÏ¿Ô£¨œ˙ €µ•º€
ÃÏ¿Ô£¨œ˙ €µ•º€![]() ‘™/«ßøÀ£¨”Î ±º‰
‘™/«ßøÀ£¨”Î ±º‰![]() £®ÃÏ£©÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™£∫
£®ÃÏ£©÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™£∫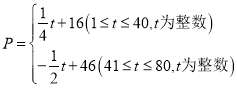 £¨»’œ˙ €¡ø
£¨»’œ˙ €¡ø![]() £®«ßøÀ£©”Î ±º‰µ⁄
£®«ßøÀ£©”Î ±º‰µ⁄![]() £®ÃÏ£©÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ æ£∫
£®ÃÏ£©÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ æ£∫
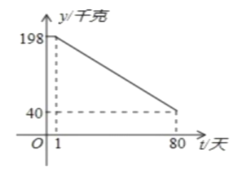
£®1£©«Û»’œ˙ €¡ø![]() ”Î ±º‰
”Î ±º‰![]() µƒ∫Ø ˝πÿœµ Ω£ø
µƒ∫Ø ˝πÿœµ Ω£ø
£®2£©ƒƒ“ªÃϵƒ»’œ˙ €¿˚»Û◊Ó¥Û£ø◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
£®3£©‘⁄ µº œ˙ €µƒ«∞![]() ÃÏ÷–£¨∏√—¯÷≥ªßæˆ∂®œ˙ €
ÃÏ÷–£¨∏√—¯÷≥ªßæˆ∂®œ˙ €![]() «ßøÀ–°¡˙œ∫£¨æÕæË‘˘
«ßøÀ–°¡˙œ∫£¨æÕæË‘˘![]() ‘™∏¯¥Â¿ÔµƒÃÿ¿ßªß£¨‘⁄’‚«∞
‘™∏¯¥Â¿ÔµƒÃÿ¿ßªß£¨‘⁄’‚«∞![]() ÃÏ÷–£¨√øÃÏø€≥˝æË‘˘∫Ûµƒ»’œ˙ €¿˚»ÛÀÊ ±º‰
ÃÏ÷–£¨√øÃÏø€≥˝æË‘˘∫Ûµƒ»’œ˙ €¿˚»ÛÀÊ ±º‰![]() µƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨«Û
µƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨«Û![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥“©≥ßœ˙ €≤ø√≈∏˘æð –≥°µ˜—–Ω·π˚£¨∂‘∏√≥ß…˙≤˙µƒ“ª÷÷–¬–Õ‘≠¡œ“©Œ¥¿¥¡ΩƒÍµƒœ˙ €Ω¯––‘§≤‚£¨≤¢Ω®¡¢»Áœ¬ƒ£–Õ£∫…˵⁄t∏ˆ‘¬∏√‘≠¡œ“©µƒ‘¬œ˙ €¡øŒ™P£®µ•Œª£∫∂÷£©£¨P”Ît÷ƺ‰¥Ê‘⁄»ÁÕºÀ˘ 浃∫Ø ˝πÿœµ£¨∆‰ÕºœÒ «∫Ø ˝P£Ω![]() £®0£ºt°Ð8£©µƒÕºœÒ”Îœþ∂ŒABµƒ◊È∫œ£ª…˵⁄t∏ˆ‘¬œ˙ €∏√‘≠¡œ“©√ø∂÷µƒ√´¿˚»ÛŒ™Q£®µ•Œª£∫ÕÚ‘™£©£¨Q”Ît÷ƺ‰¬˙◊„»Áœ¬πÿœµ£∫Q£Ω
£®0£ºt°Ð8£©µƒÕºœÒ”Îœþ∂ŒABµƒ◊È∫œ£ª…˵⁄t∏ˆ‘¬œ˙ €∏√‘≠¡œ“©√ø∂÷µƒ√´¿˚»ÛŒ™Q£®µ•Œª£∫ÕÚ‘™£©£¨Q”Ît÷ƺ‰¬˙◊„»Áœ¬πÿœµ£∫Q£Ω![]()

£®1£©µ±8£ºt°Ð24 ±£¨«ÛPπÿ”⁄tµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©…˵⁄t∏ˆ‘¬œ˙ €∏√‘≠¡œ“©µƒ‘¬√´¿˚»ÛŒ™w£®µ•Œª£∫ÕÚ‘™£©
¢Ÿ«Ûwπÿ”⁄tµƒ∫Ø ˝±Ì¥Ô Ω£ª
¢⁄Œ¥¿¥¡ΩƒÍƒ⁄£¨µ±‘¬œ˙ €¡øPŒ™ ±£¨‘¬√´¿˚»ÛŒ™w¥ÔµΩ◊Ó¥Û£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy1£Ωa£®x+2£©2©Å3”Îy2£Ω![]() £®x©Å3£©2+1Ωª”⁄µ„A(1£¨3)£¨π˝µ„A◊˜x÷·µƒ∆Ω––œþ£¨∑÷±Ωª¡ΩÃı≈◊ŒÔœþ”⁄µ„B£¨C£Æ‘Ú“‘œ¬Ω·¬€£∫¢ŸŒÞ¬€x»°∫Œ÷µ£¨y2µƒ÷µ◊Ð «’˝ ˝£ª¢⁄a£Ω
£®x©Å3£©2+1Ωª”⁄µ„A(1£¨3)£¨π˝µ„A◊˜x÷·µƒ∆Ω––œþ£¨∑÷±Ωª¡ΩÃı≈◊ŒÔœþ”⁄µ„B£¨C£Æ‘Ú“‘œ¬Ω·¬€£∫¢ŸŒÞ¬€x»°∫Œ÷µ£¨y2µƒ÷µ◊Ð «’˝ ˝£ª¢⁄a£Ω![]() £ª¢€µ±x£Ω0 ±£¨y2©Åy1£Ω6£ª¢ÐAB+AC£Ω10£ª∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝ «£® £©
£ª¢€µ±x£Ω0 ±£¨y2©Åy1£Ω6£ª¢ÐAB+AC£Ω10£ª∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝ «£® £©
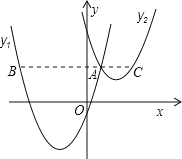
A.¢Ÿ¢⁄¢ÐB.¢Ÿ¢€¢ÐC.¢⁄¢€¢ÐD.¢Ÿ¢⁄¢€¢Ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() °¢
°¢![]() ¡Ωµ„‘⁄∑¥±»¿˝∫Ø ˝
¡Ωµ„‘⁄∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛ…œ£¨œ¬¡–»˝∏ˆ√¸Ã‚£∫¢Ÿ»Ù
µƒÕºœÛ…œ£¨œ¬¡–»˝∏ˆ√¸Ã‚£∫¢Ÿ»Ù![]() £¨‘Ú
£¨‘Ú![]() £ª¢⁄»Ù
£ª¢⁄»Ù![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() £ª¢€π˝
£ª¢€π˝![]() °¢
°¢![]() ¡Ωµ„µƒ÷±œþ”Î
¡Ωµ„µƒ÷±œþ”Î![]() ÷·°¢
÷·°¢![]() ÷·∑÷±Ωª”⁄
÷·∑÷±Ωª”⁄![]() °¢
°¢![]() ¡Ωµ„£¨¡¨Ω”
¡Ωµ„£¨¡¨Ω”![]() °¢
°¢![]() £¨‘Ú
£¨‘Ú![]() £Æ∆‰÷–’Ê√¸Ã‚∏ˆ ˝ «£® £©
£Æ∆‰÷–’Ê√¸Ã‚∏ˆ ˝ «£® £©
A.0B.1C.2D.3
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨µ„
£¨µ„![]() «
«![]() µƒ÷–µ„£¨Ω´
µƒ÷–µ„£¨Ω´![]() —ÿ
—ÿ![]() ∑≠’€µ√µΩ
∑≠’€µ√µΩ![]() £¨¡¨
£¨¡¨![]() £¨‘Úœþ∂Œ
£¨‘Úœþ∂Œ![]() µƒ≥§µ»”⁄£® £©
µƒ≥§µ»”⁄£® £©

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
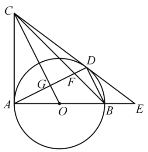
°æƒø°ø»ÁÕº£¨“—÷™ABŒ™°—Oµƒ÷±æ∂£¨ACŒ™°—Oµƒ«–œþ£¨¡¨Ω·CO£¨π˝B◊˜BD°ŒOCΩª°—O”⁄D£¨¡¨Ω·ADΩªOC”⁄G£Æ—”≥§AB°¢CDΩª”⁄µ„E£Æ
£®1£©«Û÷§£∫CD «°—Oµƒ«–œþ£ª
£®2£©»ÙBE£Ω2£¨DE£Ω4£¨«ÛCDµƒ≥§£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨¡¨Ω·BCΩªAD”⁄F£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com