
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,并建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图像是函数P=![]() (0<t≤8)的图像与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图像与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()

(1)当8<t≤24时,求P关于t的函数表达式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数表达式;
②未来两年内,当月销售量P为时,月毛利润为w达到最大.
【答案】(1)P=t+2;(2)①当0<t≤8时,w=240;当8<t≤12时,w=2t2+12t+16;当12<t≤24时,w=﹣t2+42t+88;②23
【解析】
(1)设8<t≤24时,P=kt+b,将A(8,10)、B(24,26)代入求解可得P=t+2;
(2)①分0<t≤8、8<t≤12和12<t≤24三种情况,根据月毛利润=月销量×每吨的毛利润可得函数解析式;
②当0<t≤8时,w的值始终是240;当8<t≤12时,w=2t2+12t+16=2(t+3)22,当t=12时,求得w值;当12<t≤24时,w=﹣t2+42t+88=﹣(t﹣21)2+529,根据二次函数的增减性求得当t=21时w的值,进而可得到结论.
解:(1)设8<t≤24时,P=kt+b,
将A(8,10)、B(24,26)代入,得:
![]()
解得:![]() ,
,
∴P=t+2;
(2)∵w=P·Q
∴①当0<t≤8时,w=(2t+8)×![]() =240;
=240;
当8<t≤12时,w=(2t+8) (t+2)=2t2+12t+16;
当12<t≤24时,w=(﹣t+44)(t+2)=﹣t2+42t+88;
②当0<t≤8时,w=240;
当8<t≤12时,w=2t2+12t+16=2(t+3)2﹣2,
∴8<t≤12时,w随t的增大而增大,
当t=12时,w取得最大值,最大值为448,
当12<t≤24时,w=﹣t2+42t+88=﹣(t﹣21)2+529,
当t=21时,w取得最大值529,
∵529>448>240
∴t=21时,w取得最大值
此时P=t+2=23


科目:初中数学 来源: 题型:
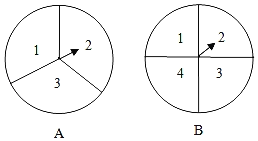
【题目】如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别标有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)若规定两个数字的积为偶数时甲赢,两个数字的积为奇数时乙赢,请问这个游戏对甲、乙两人是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解该校学生参加体育晨跑情况,随机抽查了部分学生最近两周参加跑步活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:
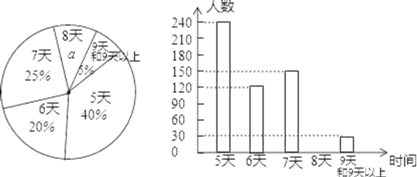
请根据图中提供的信息,回答下列问题:
(1)补全条形统计图;
(2)本次抽样调查的众数为 ,中位数为 ;
(3)如果该校约有4500名学生,请你估计全校可能有多少名学生参加体育晨跑天数不少于7天?
查看答案和解析>>
科目:初中数学 来源: 题型:
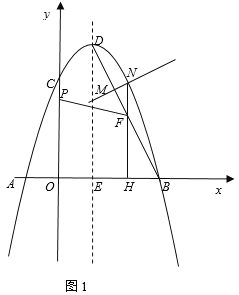
【题目】如图1,在平面直角坐标系中,抛物线y=ax2-2ax+3与x轴交于点A,B(点A在点B的左侧),交y轴于点C,点A的坐标为(-1,0),点D为抛物线的顶点,对称轴与x轴交于点E.
(1)填空:a= ,点B的坐标是 ;
(2)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD,交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当△MNF的周长取得最大值时,求FP+![]() PC的最小值;
PC的最小值;
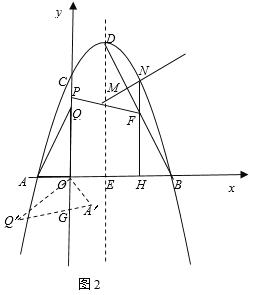
(3)在(2)中,当△MNF的周长取得最大值时,FP+![]() PC取得最小值时,如图2,把点P向下平移
PC取得最小值时,如图2,把点P向下平移![]() 个单位得到点Q,连结AQ,把△AOQ绕点O顺时针旋转一定的角度α(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G.在旋转过程中,是否存在一点G,使得GQ′=OG?若存在,请直接写出所有满足条件的点Q′的坐标;若不存在,请说明理由.
个单位得到点Q,连结AQ,把△AOQ绕点O顺时针旋转一定的角度α(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G.在旋转过程中,是否存在一点G,使得GQ′=OG?若存在,请直接写出所有满足条件的点Q′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱乐器),现将收集到的数据绘制如下的两幅不完整的统计图.
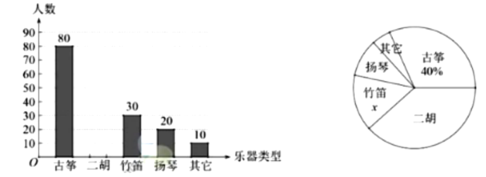
(1)这次共抽取 学生进行调查,扇形统计图中的![]() .
.
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是 度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
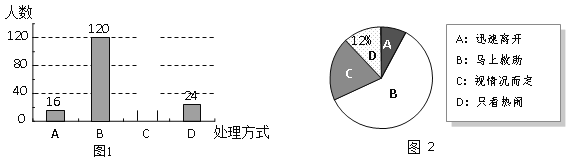
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
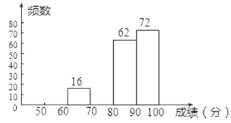
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=4x+4与x轴、y轴分别交于点A,B,抛物线y=ax2+bx-3a经过点A,将点B向右平移5个单位长度得到点C.若抛物线与线段BC恰有一个公共点,结合函数图象,a的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com