
【题目】如图,边长为1的正方形ABCD中,点E、F分别在边CD、AD上,连接BE、BF、EF,且有AF+CE=EF.
(1)求(AF+1)(CE+1)的值;
(2)探究∠EBF的度数是否为定值,并说明理由;
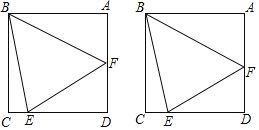
【答案】(1)2;(2)∠EBF的度数为定值,理由见解析
【解析】
(1)设CE=x,AF=y,先根据EF2=DE2+DF2推出xy+x+y=1,再用含![]() 和
和![]() 的式子表示
的式子表示![]() 并整体代值即得;
并整体代值即得;
(2)将![]() 绕点B顺时针旋转90°得到
绕点B顺时针旋转90°得到![]() ,证明
,证明![]() ,进而得出∠EBF=∠ABF+∠CBE即得.
,进而得出∠EBF=∠ABF+∠CBE即得.
解:(1)设CE=x,AF=y,则DE=1﹣x,DF=1﹣y,∵AF+CE=EF,
∴EF=x+y,∵四边形ABCD是矩形,∴∠D=90°,∴![]() ,
,
∴![]()
∴xy+x+y=1
∴![]() ;
;
(2)∠EBF的度数为定值,理由如下:
如图1,将![]() 绕点B顺时针旋转90°得到
绕点B顺时针旋转90°得到![]() ,此时AB与CB重合.
,此时AB与CB重合.
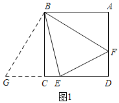
由旋转可得AB=BC,BF=BG,∠ABF=∠CBG,∠BCG=∠A=90°.
∴∠BCG+∠BCD=90°+90°=180°.∴点G、C、E在同一条直线上.
∵AF+CE=EF=CG+CE=EG,
∵BE=BE
∴![]()
∴∠EBF=∠EBG=∠CBG+∠CBE=∠ABF+∠CBE,
∵∠ABC=90°,∴∠EBF=45°
∴∠EBF的度数为定值;


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
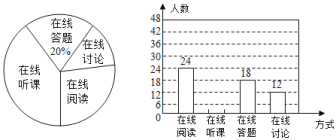
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生2100人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田赛项目:跳远,跳高
;田赛项目:跳远,跳高![]() 分别用
分别用![]() 、
、![]() 表示
表示![]() .
.
![]() 该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
![]() 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取![]() 名学生,对每人每周用于课外阅读的平均时间(单位:
名学生,对每人每周用于课外阅读的平均时间(单位:![]() )进行调查,过程如下:
)进行调查,过程如下:
收集数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理数据:
课外阅读平均时间 |
|
|
|
|
等级 |
|
|
|
|
人数 |
|
|
|
|
分析数据:
平均数 | 中位数 | 众数 |
|
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(2)已知该校学生![]() 人,若每人每周用于课外阅读的平均时间不少于
人,若每人每周用于课外阅读的平均时间不少于![]() 为达标,请估计达标的学生数;
为达标,请估计达标的学生数;
查看答案和解析>>
科目:初中数学 来源: 题型:
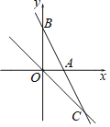
【题目】如图,在平面直角坐标系中,直线y=﹣2x+4与x轴交于点A,与y轴交于点B,与直线y=kx交于点C(4,n),则tan∠OCB的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
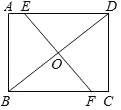
【题目】如图,在矩形ABCD中,EF经过对角线BD的中点O,分别交AD,BC于点E,F
(1)求证:△BOF≌△DOE;
(2)若AB=4cm,AD=5cm,当EF⊥BD时,求四边形ABFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点E,在弦BC上取一点F,使AF=AE,连接AF并延长交⊙O于点D.
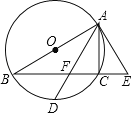
(1)求证:∠B=∠CAD;
(2)若CE=2,∠B=30°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.

根据以上信息,解答下列问题:
(1)甲同学所列方程中的![]() 表示_________________;乙同学所列方程中的
表示_________________;乙同学所列方程中的![]() 表示________________;
表示________________;
(2)两个方程中任选一个,解方程并回答老师提出的问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com