
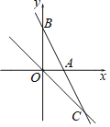
【题目】如图,在平面直角坐标系中,直线y=﹣2x+4与x轴交于点A,与y轴交于点B,与直线y=kx交于点C(4,n),则tan∠OCB的值为_________.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
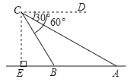
【题目】如图,一架无人机航拍过程中在![]() 处测得地面上
处测得地面上![]() ,
,![]() 两个目标点的俯角分别为
两个目标点的俯角分别为![]() 和
和![]() .若
.若![]() ,
,![]() 两个目标点之间的距离是100米,则此时无人机与目标点
两个目标点之间的距离是100米,则此时无人机与目标点![]() 之间的距离(即
之间的距离(即![]() 的长)为( )
的长)为( )
A.100米B.![]() 米C.50米D.
米C.50米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
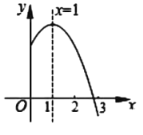
【题目】已知二次函数![]() (
(![]() 是常数,
是常数,![]() )图象的对称轴是直线
)图象的对称轴是直线![]() ,其图象的一部分如图所示,下列说法中①
,其图象的一部分如图所示,下列说法中①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() ;⑤
;⑤![]() .正确的结论有( )
.正确的结论有( )
A.①②④B.②③④C.①③⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
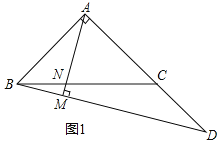
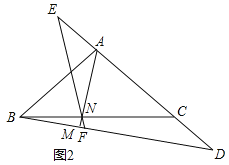
【题目】如图,在![]() 中,
中,![]() ,点D为AC延长线上一点,连接BD,过A作
,点D为AC延长线上一点,连接BD,过A作![]() ,垂足为M,交BC于点N
,垂足为M,交BC于点N
![]() 如图1,若
如图1,若![]() ,
,![]() ,求AM的长;
,求AM的长;
![]() 如图2,点E在CA的延长线上,且
如图2,点E在CA的延长线上,且![]() ,连接EN并延长交BD于点F,求证:
,连接EN并延长交BD于点F,求证:![]() ;
;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,请求出
时,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
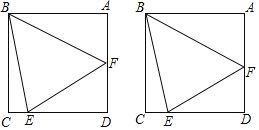
【题目】如图,边长为1的正方形ABCD中,点E、F分别在边CD、AD上,连接BE、BF、EF,且有AF+CE=EF.
(1)求(AF+1)(CE+1)的值;
(2)探究∠EBF的度数是否为定值,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙虾狂欢季再度开启,第![]() 届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为
届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为![]() 元,在整个销售旺季的
元,在整个销售旺季的![]() 天里,销售单价
天里,销售单价![]() 元/千克,与时间
元/千克,与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: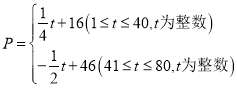 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
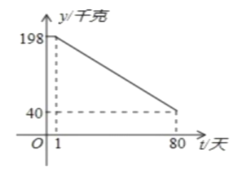
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前![]() 天中,该养殖户决定销售
天中,该养殖户决定销售![]() 千克小龙虾,就捐赠
千克小龙虾,就捐赠![]() 元给村里的特困户,在这前
元给村里的特困户,在这前![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com