
【题目】下图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.

根据以上信息,解答下列问题:
(1)甲同学所列方程中的![]() 表示_________________;乙同学所列方程中的
表示_________________;乙同学所列方程中的![]() 表示________________;
表示________________;
(2)两个方程中任选一个,解方程并回答老师提出的问题.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
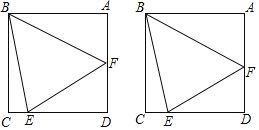
【题目】如图,边长为1的正方形ABCD中,点E、F分别在边CD、AD上,连接BE、BF、EF,且有AF+CE=EF.
(1)求(AF+1)(CE+1)的值;
(2)探究∠EBF的度数是否为定值,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①为汽车沿直线运动的速度v(m/s)与时间t(s)(0≤t≤40)之间的函数图象.根据对此图象的分析、理解,在图②中画出描述在这段时间内汽车离开出发点的路程s(m)与时间t(s)之间的函数图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+(4a﹣1)x﹣4与x轴交于点A、B,与y轴交于点C,且OC=2OB,点D为线段OB上一动点(不与点B重合),过点D作矩形DEFH,点H、F在抛物线上,点E在x轴上.
(1)求抛物线的解析式;
(2)当矩形DEFH的周长最大时,求矩形DEFH的面积;
(3)在(2)的条件下,矩形DEFH不动,将抛物线沿着x轴向左平移m个单位,抛物线与矩形DEFH的边交于点M、N,连接M、N.若MN恰好平分矩形DEFH的面积,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小龙虾养殖大户为了更好地发挥技术优势,一次性收购了20000kg小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批小龙虾放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
![]() 求出抛物线的对称轴方程以及与
求出抛物线的对称轴方程以及与![]() 轴的交点坐标
轴的交点坐标
![]() 当
当![]() 时,求出抛物线与
时,求出抛物线与![]() 轴的交点坐标
轴的交点坐标
![]() 已知
已知![]() 三点构成三角形
三点构成三角形![]() ,当抛物线与三角形
,当抛物线与三角形![]() 的三条边一共有
的三条边一共有![]() 个交点时,直接写出
个交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
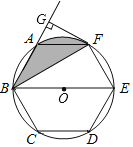
【题目】如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB为⊙O的直径,C,D为⊙O上两点,过点D的直线EF与⊙O相切,分别交BA,BC的延长线于点E,F,BF⊥EF
(I)如图①,若∠ABC=50°,求∠DBC的大小;
(Ⅱ)如图②,若BC=2,AB=4,求DE的长.
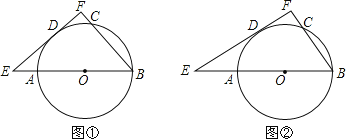
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com