
【题目】已知,AB为⊙O的直径,C,D为⊙O上两点,过点D的直线EF与⊙O相切,分别交BA,BC的延长线于点E,F,BF⊥EF
(I)如图①,若∠ABC=50°,求∠DBC的大小;
(Ⅱ)如图②,若BC=2,AB=4,求DE的长.
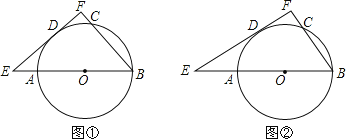
【答案】(1)25°;(2)2![]() .
.
【解析】
(1)如图1,连接OD,BD,由EF与⊙O相切,得到OD⊥EF,由于BF⊥EF,得到OD∥BF,得到∠AOD=∠ABC=50°,由外角的性质得到结果;
(2)如图2,连接AC,OD,根据AB为⊙O的直径,得出∠ACB=90°,由直角三角形的性质得到∠CAB=30°,于是AC=ABcos30°=4×![]() =2
=2![]() ,AH=AOcos30°=2×
,AH=AOcos30°=2×![]() =
=![]() ,根据三角形的中位线的性质解得结果.
,根据三角形的中位线的性质解得结果.
解(1)如图1,连接OD,BD,
∵EF与⊙O相切,
∴OD⊥EF,
∵BF⊥EF,
∴OD∥BF,
∴∠AOD=∠ABC=50°,
∵OD=OB,
∴∠OBD=∠ODB=![]() ∠AOD=25°
∠AOD=25°
∴∠DBC=∠OBC-∠OBD=25°;
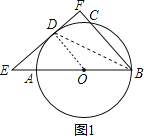
(2)如图2,连接AC,OD,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=2,AB=4,
∴∠CAB=30°,
∴AC=ABcos30°=4×![]() =2
=2![]() ,
,
∵∠ODF=∠F=∠HCO=90°,
∴∠DHC=90°,
∴AH=AOcos30°=2×![]() =
=![]() ,
,
∵∠HAO=30°,
∴OH=![]() OA=
OA=![]() OD,
OD,
∵AC∥EF,
∴DE=2AH=2![]() .
.


科目:初中数学 来源: 题型:
【题目】下图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.

根据以上信息,解答下列问题:
(1)甲同学所列方程中的![]() 表示_________________;乙同学所列方程中的
表示_________________;乙同学所列方程中的![]() 表示________________;
表示________________;
(2)两个方程中任选一个,解方程并回答老师提出的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .对于下列结论:
.对于下列结论:
①![]() ;②
;②![]() ;③
;③![]() .其中正确的是( )
.其中正确的是( )
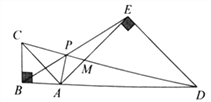
A. ①②③ B. ① C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
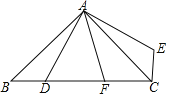
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
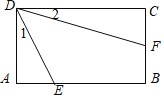
【题目】如图,矩形ABCD长与宽的比为3:2,点E,F分别在边AB、BC上,tan∠1=![]() ,tan∠2=
,tan∠2=![]() ,则cos(∠1+∠2)=( )
,则cos(∠1+∠2)=( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
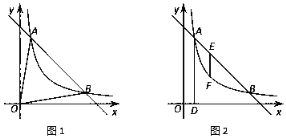
【题目】如图1,点A(m,6),B(6,1)在反比例函数图象上,作直线AB,连接OA、OB.
(1)求反比例函数的表达式和m的值;
(2)求△AOB的面积;
(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作x轴的垂线,交反比例函数图象于点F,若EF=![]() AD,求出点E的坐标.
AD,求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在三角形![]() 中,
中,![]() ,
,![]() 和
和![]() 关于
关于![]() 对称
对称
(1)将图1中的![]() 以
以![]() 为旋转中心,逆时针方向旋转角
为旋转中心,逆时针方向旋转角![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长
,分别延长![]() 和
和![]() 交于点
交于点![]() ,则四边形
,则四边形![]() 的形状是 ;
的形状是 ;
(2)将图1中的![]() 以
以![]() 为旋转中心,按逆时针方向旋转角
为旋转中心,按逆时针方向旋转角![]() ,使
,使![]() ,得到如图3所示的
,得到如图3所示的![]() ,连接
,连接![]() 和
和![]() ,得到四边形
,得到四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图3中,![]() ,将
,将![]() 沿着射线
沿着射线![]() 方向平移
方向平移![]() ,得到
,得到![]() ,连接
,连接![]() ,使四边形
,使四边形![]() 恰好为正方形,请直接写出a的值.
恰好为正方形,请直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
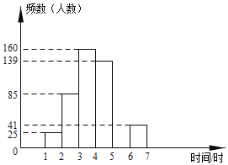
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com