
【题目】如图1,在三角形![]() 中,
中,![]() ,
,![]() 和
和![]() 关于
关于![]() 对称
对称
(1)将图1中的![]() 以
以![]() 为旋转中心,逆时针方向旋转角
为旋转中心,逆时针方向旋转角![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长
,分别延长![]() 和
和![]() 交于点
交于点![]() ,则四边形
,则四边形![]() 的形状是 ;
的形状是 ;
(2)将图1中的![]() 以
以![]() 为旋转中心,按逆时针方向旋转角
为旋转中心,按逆时针方向旋转角![]() ,使
,使![]() ,得到如图3所示的
,得到如图3所示的![]() ,连接
,连接![]() 和
和![]() ,得到四边形
,得到四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图3中,![]() ,将
,将![]() 沿着射线
沿着射线![]() 方向平移
方向平移![]() ,得到
,得到![]() ,连接
,连接![]() ,使四边形
,使四边形![]() 恰好为正方形,请直接写出a的值.
恰好为正方形,请直接写出a的值.

【答案】(1)菱形;(2)四边形BCC′D是矩形,理由见解析;(3)a的值为![]() 或
或![]() .
.
【解析】
(1)由对称的性质结合题意得出DC=BC=DA=AB,∠BAC=∠DAC=∠BCA=∠DCA,由旋转的性质得出∠CAC′=∠BAC=∠AC′D=∠BCA,证出AC∥DE,AC′∥BE,得出四边形ACEC′是平行四边形,由旋转可得:AC=AC′,即可得出四边形ACEC′是菱形;
(2)过点A作AE⊥C′C于点E,由旋转的性质,得AC′=AC,得出∠CAE=∠C′AE=![]() α=∠BAC,∠AEC′=90°,由等腰三角形的性质得出∠BCA=∠BAC,进而得出∠CAE=∠BCA,证出AE∥BC.同理,AE∥DC′,得出BC∥DC′,证出四边形BCC′D是平行四边形,求出∠BCC'=90°,即可得出四边形BCC′D是矩形;
α=∠BAC,∠AEC′=90°,由等腰三角形的性质得出∠BCA=∠BAC,进而得出∠CAE=∠BCA,证出AE∥BC.同理,AE∥DC′,得出BC∥DC′,证出四边形BCC′D是平行四边形,求出∠BCC'=90°,即可得出四边形BCC′D是矩形;
(3)过点B作BF⊥AC于F,证明△ACE∽△CBF,得出![]() ,求出CE=
,求出CE=![]() ,由等腰三角形的性质得出CC′=2CE=
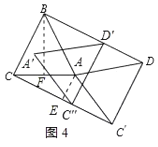
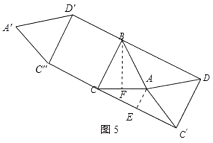
,由等腰三角形的性质得出CC′=2CE=![]() ,当四边形BCC′'D′恰好为正方形时,分两种情况:①C′'在边CC′上时,a=CC′CC';②当点C′'在C′C的延长线上时,a=CC′+CC'.
,当四边形BCC′'D′恰好为正方形时,分两种情况:①C′'在边CC′上时,a=CC′CC';②当点C′'在C′C的延长线上时,a=CC′+CC'.
解:(1)∵△ADC和△ABC关于AC对称,
∴DC=BC,DA=AB,∠BAC=∠DAC,∠BCA=∠DCA,
∵BA=BC,
∴DC=BC=DA=AB,∠BAC=∠DAC=∠BCA=∠DCA,
∵△ACD以A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到△AC′D,
∴∠CAC′=∠BAC=∠AC′D=∠BCA,
∴AC∥DE,AC′∥BE,
∴四边形ACEC′是平行四边形,
由旋转可得:AC=AC′,
∴四边形ACEC′是菱形,
故答案为:菱形;
(2)四边形BCC′D是矩形;
理由:过点A作AE⊥C′C于点E,如图3所示:

由旋转的性质,得AC′=AC,
∴∠CAE=∠C′AE=![]() α=∠BAC,∠AEC′=90°,
α=∠BAC,∠AEC′=90°,
∵BA=BC,
∴∠BCA=∠BAC,
∴∠CAE=∠BCA,
∴AE∥BC,
同理,AE∥DC′,
∴BC∥DC′,
∵BC=DC′,
∴四边形BCC′D是平行四边形,
∵AE∥BC,∠AEC′=90°,
∴∠BCC′=90°,
∴四边形BCC′D是矩形;
(3)过点B作BF⊥AC于F,
∵BA=BC,
∴CF=AF![]() AC=
AC=![]() ×10=5,
×10=5,
在Rt△BCF中,BF=![]() ,
,
∵∠CAE=∠BCF,∠CEA=∠BFC=90°,
∴△ACE∽△CBF,
∴![]() ,即
,即![]() ,
,
解得:CE=![]() ,
,
∵AC=AC′,AE⊥CC′,
∴CC′=2CE=![]() ,
,
当四边形BCC′'D′恰好为正方形时,CC'=BC=![]() ,
,
分两种情况:①C′'在边CC′上时,如图4所示:
则a=CC′CC'=![]() ;
;
②当点C′'在C′C的延长线上时,如图5所示:
则a=CC′+CC'=![]() ;
;
综上所述,a的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
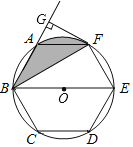
【题目】如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB为⊙O的直径,C,D为⊙O上两点,过点D的直线EF与⊙O相切,分别交BA,BC的延长线于点E,F,BF⊥EF
(I)如图①,若∠ABC=50°,求∠DBC的大小;
(Ⅱ)如图②,若BC=2,AB=4,求DE的长.
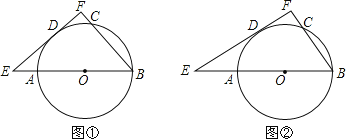
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年,9月3日全国各地将举行有关纪念活动.为了解初中学生对二战历史的知晓情况,某初中课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类,其中
四类,其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”;
类表示“基本了解”;![]() 类表示“不太了解”,调查的数据经整理后形成尚未完成的条形统计图(如图①)和扇形统计图(如图②):
类表示“不太了解”,调查的数据经整理后形成尚未完成的条形统计图(如图①)和扇形统计图(如图②):
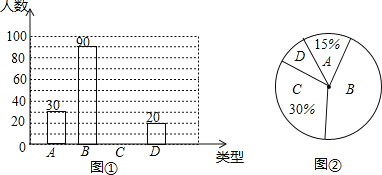
(1)在这次抽样调查中,一共抽查了 名学生;
(2)请把图①中的条形统计图补充完整;
(3)图②的扇形统计图中![]() 类部分所对应扇形的圆心角的度数为 ;
类部分所对应扇形的圆心角的度数为 ;
(4)如果这所学校共有初中学生1500名,请你估算该校初中学生中对二战历史“非常了解”和“比较了解”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
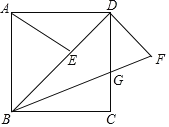
【题目】如图,在正方形ABCD中,点E是对角线BD上一点,连接AE,将DE绕D点逆时针方向旋转90°到DF,连接BF,交DC于点G,若DG=3,CG=2,则线段AE的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接”抗战胜利70周年纪念展”,中国国家博物馆进行了合并改扩建工程.新馆的展厅总面积与原馆大楼的总建筑面积相同,成为目前世界上最大的博物馆.已知原馆大楼的总建筑面积比原馆大楼的展览面积的3倍少0.4万平方米,新馆的展厅总面积比原馆大楼的展览面积大4.2万平方米,求新馆的展厅总面积和原馆大楼的展览面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c(b,c为常数)与x轴交于点(x1,0)和(x2,0),与y轴交于点A,点E为抛物线顶点.
(Ⅰ)当x1=﹣1,x2=3时,求点E,点A的坐标;
(Ⅱ)①若顶点E在直线y=x上时,用含有b的代数式表示c;
②在①的前提下,当点A的位置最高时,求抛物线的解析式;
(Ⅲ)若x1=﹣1,b>0,当P(1,0)满足PA+PE值最小时,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段AB及一定点C、P是线段AB上一动点,作直线CP,过点A作AQ⊥CP于点Q,已知AB=7cm,设A、P两点间的距离为xcm,A、Q两点间的距离为y1cm,P、Q两点间的距离为y2cm.小明根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:
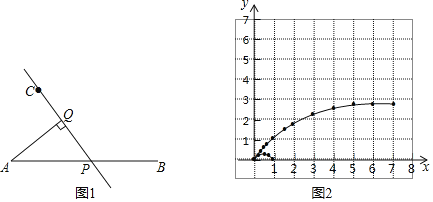
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值.
x/cm | 0 | 0.3 | 0.5 | 0.8 | 1 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 |
y1/cm | 0 | 0.28 | 0.49 | 0.79 | 1 | 1.48 | 1.87 | 2.37 | 2.61 | 2.72 | 2.76 | 2.78 |
y2/cm | 0 | 0.08 | 0.09 | 0.06 | 0 | 0.29 | 0.73 | 1.82 |
| 4.20 | 5.33 | 6.41 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,解决问题:当△APQ中有一个角为30°时,AP的长度约为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com