
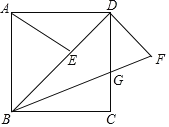
【题目】如图,在正方形ABCD中,点E是对角线BD上一点,连接AE,将DE绕D点逆时针方向旋转90°到DF,连接BF,交DC于点G,若DG=3,CG=2,则线段AE的长为__.
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
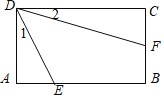
【题目】如图,矩形ABCD长与宽的比为3:2,点E,F分别在边AB、BC上,tan∠1=![]() ,tan∠2=
,tan∠2=![]() ,则cos(∠1+∠2)=( )
,则cos(∠1+∠2)=( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在三角形![]() 中,
中,![]() ,
,![]() 和
和![]() 关于
关于![]() 对称
对称
(1)将图1中的![]() 以
以![]() 为旋转中心,逆时针方向旋转角
为旋转中心,逆时针方向旋转角![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长
,分别延长![]() 和
和![]() 交于点
交于点![]() ,则四边形
,则四边形![]() 的形状是 ;
的形状是 ;
(2)将图1中的![]() 以
以![]() 为旋转中心,按逆时针方向旋转角
为旋转中心,按逆时针方向旋转角![]() ,使
,使![]() ,得到如图3所示的
,得到如图3所示的![]() ,连接
,连接![]() 和
和![]() ,得到四边形
,得到四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图3中,![]() ,将
,将![]() 沿着射线
沿着射线![]() 方向平移
方向平移![]() ,得到
,得到![]() ,连接
,连接![]() ,使四边形
,使四边形![]() 恰好为正方形,请直接写出a的值.
恰好为正方形,请直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从少年宫出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,则乙在途中等候甲用了( )秒
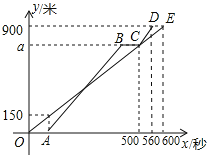
A.200B.150C.100D.80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桃花中学计划购买![]() 两种型号的小黑板,经洽谈, 购买一块
两种型号的小黑板,经洽谈, 购买一块![]() 型小黑板比买一块
型小黑板比买一块![]() 型小黑板多
型小黑板多![]() 元,且购买
元,且购买![]() 块
块![]() 型小黑板和
型小黑板和![]() 块
块![]() 型小黑板共需
型小黑板共需![]() 元.
元.
(1)求购买一块![]() 型小黑板和一块
型小黑板和一块![]() 型小黑板各需要多少元?
型小黑板各需要多少元?
(2)根据学校的实际情况,需购买![]() 两种型号的小黑板共
两种型号的小黑板共![]() 块,并且购买
块,并且购买![]() 型小黑板的数量不少于购买
型小黑板的数量不少于购买![]() 型小黑板的数量,请问学校购买这批小黑板最少要多少元?
型小黑板的数量,请问学校购买这批小黑板最少要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有M、N两点,M点表示的数分别为m,N点表示的数是n(n>m),则线段MN的长(点M到点N的距离)可表示为MN=n﹣m,请用上面材料中的知识解答下面的问题:一个点从数轴上的原点O开始,先向左移动3cm到达A点,再向右移动2cm到达B点,然后向右移动4cm到达C点,用1cm表示1个单位长度.
(1)请你在数轴上表示出A、B、C三点的位置,并直接写出线段AC的长度.
(2)若数轴上有一点D,且AD=4cm,则点D表示的数是什么?
(3)若将点A向右移动xcm,请用代数式表示移动后的点所表示的数.
(4)若点P以从点A向原点O移动,同时点Q以与点P相同的速度从原点O向点C移动,试探索:PQ的长是否会发生改变?如果不变,请求出PQ的长.如果改变,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com