
【题目】抛物线y=﹣x2+bx+c(b,c为常数)与x轴交于点(x1,0)和(x2,0),与y轴交于点A,点E为抛物线顶点.
(Ⅰ)当x1=﹣1,x2=3时,求点E,点A的坐标;
(Ⅱ)①若顶点E在直线y=x上时,用含有b的代数式表示c;
②在①的前提下,当点A的位置最高时,求抛物线的解析式;
(Ⅲ)若x1=﹣1,b>0,当P(1,0)满足PA+PE值最小时,求b的值.
【答案】(Ⅰ)点A的坐标为(0,3),点E的坐标为(1,4);(Ⅱ)①c=![]() ;②
;②![]() ;(Ⅲ)3+
;(Ⅲ)3+![]() .
.
【解析】
(Ⅰ)根据题意和x1=﹣1,x2=3,可以得到点(﹣1,0),(3,0)在抛物线y=﹣x2+bx+c的图象上,然后即可求得该抛物线的解析式,再将抛物线解析式化为顶点式,即可得到点A和点E的坐标;
(Ⅱ)①将题目中的函数解析式化为顶点式,再根据题目中顶点E在直线y=x上,即可得到c和b的关系;
②根据①的结果和二次函数的性质,可以求得当点A的位置最高时,抛物线的解析式;
(Ⅲ)根据x1=﹣1,b>0和题目中的函数解析式,可以得到点A的坐标,然后即可求得直线AP的解析式,再根据最短路线问题可以得到当P(1,0)满足PA+PE值最小时b的值.
解:(Ⅰ)∵抛物线y=﹣x2+bx+c(b,c为常数)与x轴交于点(x1,0)和(x2,0),与y轴交于点A,点E为抛物线顶点,x1=﹣1,x2=3,
∴点(﹣1,0),(3,0)在抛物线y=﹣x2+bx+c的图象上,
∴![]() ,解得
,解得![]() ,
,
∴y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴点A的坐标为(0,3),点E的坐标为(1,4);
(Ⅱ)①∵y=﹣x2+bx+c=![]() ,
,
∴点E的坐标为(![]() ,
,![]() ),
),
∵顶点E在直线y=x上,
∴![]() =
=![]() ,
,
∴c=![]() ;
;
②由①知,![]() ,
,
则点A的坐标为(0,![]() ),
),
∴当b=1时,此时点A的位置最高,函数y=﹣x2+x+![]() ,
,
即在①的前提下,当点A的位置最高时,抛物线的解析式是![]() ;
;
(Ⅲ)∵x1=﹣1,抛物线y=﹣x2+bx+c过点(x1,0),
∴﹣1﹣b+c=0,
∴c=1+b,
∵点E的坐标为(![]() ,
,![]() ),点A的坐标为(0,c),
),点A的坐标为(0,c),
∴E(![]() ,
,![]() ),A(0,b+1),
),A(0,b+1),
∴点E关于x轴的对称点E′(![]() ,﹣
,﹣![]() ),
),
设过点A(0,b+1)、P(1,0)的直线解析式为y=kx+t,
![]() ,得
,得![]() ,
,
∴直线AP的解析式为y=(﹣b﹣1)x+(b+1)=﹣(b+1)x+(b+1)=(b+1)(﹣x+1),
∵当直线AP过点E′时,PA+PE值最小,
∴﹣![]() =(b+1)(﹣
=(b+1)(﹣![]() +1),
+1),
化简得:b2﹣6b﹣8=0,
解得:b1=![]() ,b2=
,b2=![]()
∵b>0,
∴b=![]() ,
,
即b的值是3+![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在三角形![]() 中,
中,![]() ,
,![]() 和
和![]() 关于
关于![]() 对称
对称
(1)将图1中的![]() 以
以![]() 为旋转中心,逆时针方向旋转角
为旋转中心,逆时针方向旋转角![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长
,分别延长![]() 和
和![]() 交于点
交于点![]() ,则四边形
,则四边形![]() 的形状是 ;
的形状是 ;
(2)将图1中的![]() 以
以![]() 为旋转中心,按逆时针方向旋转角
为旋转中心,按逆时针方向旋转角![]() ,使
,使![]() ,得到如图3所示的
,得到如图3所示的![]() ,连接
,连接![]() 和
和![]() ,得到四边形
,得到四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图3中,![]() ,将
,将![]() 沿着射线
沿着射线![]() 方向平移
方向平移![]() ,得到
,得到![]() ,连接
,连接![]() ,使四边形
,使四边形![]() 恰好为正方形,请直接写出a的值.
恰好为正方形,请直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 有两个不同的交点.下列结论:①
有两个不同的交点.下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则
有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桃花中学计划购买![]() 两种型号的小黑板,经洽谈, 购买一块
两种型号的小黑板,经洽谈, 购买一块![]() 型小黑板比买一块
型小黑板比买一块![]() 型小黑板多
型小黑板多![]() 元,且购买
元,且购买![]() 块
块![]() 型小黑板和
型小黑板和![]() 块
块![]() 型小黑板共需
型小黑板共需![]() 元.
元.
(1)求购买一块![]() 型小黑板和一块
型小黑板和一块![]() 型小黑板各需要多少元?
型小黑板各需要多少元?
(2)根据学校的实际情况,需购买![]() 两种型号的小黑板共
两种型号的小黑板共![]() 块,并且购买
块,并且购买![]() 型小黑板的数量不少于购买
型小黑板的数量不少于购买![]() 型小黑板的数量,请问学校购买这批小黑板最少要多少元?
型小黑板的数量,请问学校购买这批小黑板最少要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
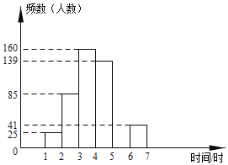
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 和
和![]() 是一次函数
是一次函数![]() 与反比例函数
与反比例函数![]() 图象的两个不同交点,点
图象的两个不同交点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 以及
以及![]() 分别与
分别与![]() 轴交与点
轴交与点![]() 和点
和点![]() .
.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)若![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数y=k1x+![]() ,且k1k2≠0,自变量x与函数值y满足以下表格:
,且k1k2≠0,自变量x与函数值y满足以下表格:
x | …… | -4 | -3 | -2 | -1 | - |
| 1 | 2 | 3 | 4 | …… |
y | …… | -3 | -2 | -1 | 0 | 1 | -1 | 0 | 1 | m | n | …… |
(1)根据表格直接写出y与x的函数表达式及自变量x的取值范围______
(2)补全上面表格:m=______,n=______;在如图所示的平面直角坐标系中,请根据表格中的数据补全y关于x的函数图象;
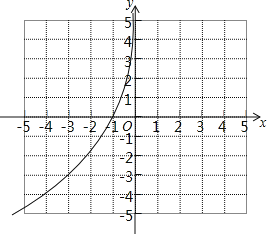
(3)结合函数图象,解决下列问题:
①写出函数y的一条性质:______;
②当函数值y≥![]() 时,x的取值范围是______;
时,x的取值范围是______;
③当函数值y=-x时,结合图象请估算x的值为______(结果保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com