Question

【题目】如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.

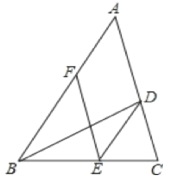
(1)求证：BE=AF；

(2)若∠ABC=60°，BD=6，求四边形ADEF的面积。

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）由DE∥AB，EF∥AC，可证得四边形ADEF是平行四边形，∠ABD=∠BDE，又由BD是△ABC的角平分线，易得△BDE是等腰三角形，即可证得结论；

（2）首先过点D作DG⊥AB于点G，过点E作EH⊥BD于点H，易求得DG与DE的长，继而求得答案．

(1)证明：∵DE∥AB,EF∥AC，

∴四边形ADEF是平行四边形，∠ABD=∠BDE，

∴AF=DE，

∵BD是△ABC的角平分线，

∴∠ABD=∠DBE，

∴∠DBE=∠BDE，

∴BE=DE，

∴BE=AF；

(2)过点D作DG⊥AB于点G，过点E作EH⊥BD于点H，

∵∠ABC=60°，BD是∠ABC的平分线，

∴∠ABD=∠EBD=30°，

∴DG=BD=×6=3，

∵BE=DE，

∴BH=DH=BD=3，

∴BE= =2，

∴DE=BE=2 ，

∴四边形ADEF的面积为：DEDG=6.