
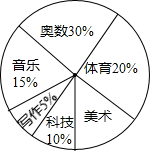
 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.| 学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
| 人数 | 72 | 36 | 54 | 18 |
分析 (1)根据总人数=参加某项的人数÷所占比例即可得出答案;
(2)根据扇形统计图直接反映部分占总体的百分比大小易得参加美术学习小组的人数和奥数小组的有人数;
(3)(4)利用(2)中所求数据,根据中位数,众数的求法易得答案.
解答 解:(1)读图可知:有10%的学生即36人参加科技学习小组,
故七年级共有学生:36÷10%=360(人).
故答案为:360;
(2)统计图中美术占:1-30%-20%-10%-15%-5%=20%,
参加美术学习小组的有:
360×(1-30%-20%-10%-15%-5%)=360×20%=72(人),
奥数小组的有360×30%=108(人);
| 学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
| 人数 | 72 | 72 | 36 | 54 | 18 | 108 |
点评 此题主要考查了扇形统计图的应用和中位数以及众数的定义,熟练掌握一组数据中出现次数最多的数为这组数据的众数;一组数据按顺序排列后,中间的那两个数的平均数或中间的那个数叫做中位数是解题关键.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:选择题
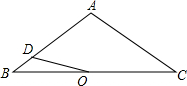 如图,△ABC中,AB=AC=4,∠BAC=120°.点O是BC中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,OD长为y.则函数y的图象大致为( )
如图,△ABC中,AB=AC=4,∠BAC=120°.点O是BC中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,OD长为y.则函数y的图象大致为( )| A. | 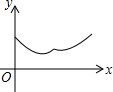 | B. | 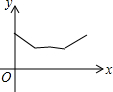 | C. | 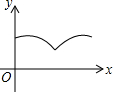 | D. | 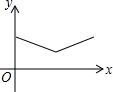 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
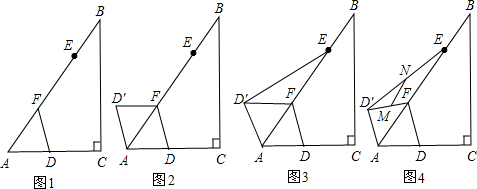
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
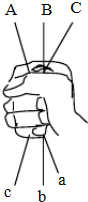 如图,晓明手里拿着三根绳子,小丽负责将两个绳头(大写字母)接好,小菊负责把两个绳尾(小写字母)接好,然后晓明把手松开,他俩正好结成一个环形的概率是多少?(请用树状图或图表分析)
如图,晓明手里拿着三根绳子,小丽负责将两个绳头(大写字母)接好,小菊负责把两个绳尾(小写字母)接好,然后晓明把手松开,他俩正好结成一个环形的概率是多少?(请用树状图或图表分析)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
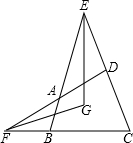 如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADC=60°,∠ABC=80°.
如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADC=60°,∠ABC=80°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
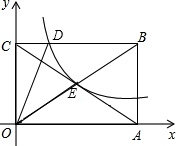 如图,反比例函数y=$\frac{k}{x}$在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
如图,反比例函数y=$\frac{k}{x}$在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
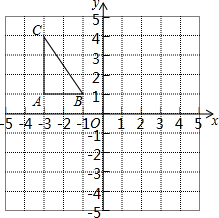 如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com