
分析 把P点代入y=-$\frac{3}{x}$求得P的坐标,进而求得OP的长,即可求得Q的坐标,从而求得k的值.
解答 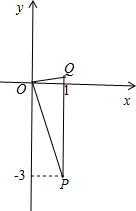 解:∵点P(1,t)在反比例函数y=-$\frac{3}{x}$的图象上,
解:∵点P(1,t)在反比例函数y=-$\frac{3}{x}$的图象上,
∴t=-$\frac{3}{1}$=-3,
∴P(1,-3),
∴OP=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵过点P作直线l与y轴平行,点Q在直线l上,满足QP=OP.
∴Q(1,$\sqrt{10}$-3)或(1,-$\sqrt{10}$-3)
∵反比例函数y=$\frac{k}{x}$的图象经过点Q,
∴$\sqrt{10}$-3=$\frac{k}{1}$或-$\sqrt{10}$-3=$\frac{k}{1}$,解得k=$\sqrt{10}$-3或-$\sqrt{10}$-3,
故答案为$\sqrt{10}$-3或-$\sqrt{10}$-3.
点评 本题考查了反比例函数图象上点的坐标特征,勾股定理的应用,求得Q点的坐标是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
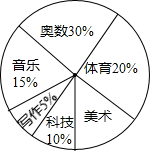 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.| 学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
| 人数 | 72 | 36 | 54 | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | -1 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
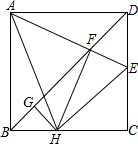 如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).
如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<3 | B. | m>3 | C. | m<0 | D. | m>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com