
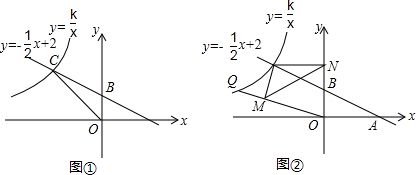
分析 (1)先求出点A、B的坐标,再由三角形COA的面积求出点C纵坐标,代入直线解析式求出点C的横坐标,把C(-4,4)代入y=$\frac{k}{x}$,即可确定k的值;
(2)作NE⊥MC于E,作NF⊥OM于F,作CG⊥x轴于G;则四边形CGON是正方形,证明C、M、O、N四点共圆,证出MF=NF,再证明四边形EMFN是正方形,得出ME=MF,MN=$\sqrt{2}$MF,由Rt△CNE≌Rt△ONF,得出CE=OF,MC+MO=2MF,即可得出结论.
解答 解:(1)对于直线y=-$\frac{1}{2}$x+2,当y=0时,x=4;当x=0时,y=2;
∴A(4,0),B(0,2),
设C(a,b),
∵S△COA=$\frac{1}{2}$×4×b=8,
∴b=4,
把C(a,4)代入y=-$\frac{1}{2}$x+2得:a=-4,
∴C(-4,4),
把C(-4,4)代入y=$\frac{k}{x}$得:
k=-16,;
(2)$\frac{MC+MO}{MN}$=$\sqrt{2}$,没有变化;理由如下:
如图所示: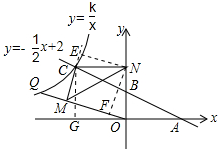 作NE⊥MC于E,作NF⊥OM于F,作CG⊥x轴于G;
作NE⊥MC于E,作NF⊥OM于F,作CG⊥x轴于G;
则四边形CGON是正方形,∠CMF=∠MFN=∠NEM=90°,
∴四边形EMFN是矩形,CG=OG=ON=CN=4,∠OCN=∠CON=45°,
∵CM⊥OQ,CN⊥y轴,
∴∠CMO=∠CNO=90°,
∴C、M、O、N四点共圆,
∴∠OMN=∠OCN=45°,∠CMN=∠NOC=45°,
∴MF=NF,
∴四边形EMFN是正方形,
∴ME=MF=FN=EN,MN=$\sqrt{2}$MF,
在Rt△CNE和Rt△ONF中,
$\left\{\begin{array}{l}{CN=ON}\\{EN=FN}\end{array}\right.$,
∴Rt△CNE≌Rt△ONF(HL),
∴CE=OF,
∴MC+MO=MC+MF+OF=2MF,
∴$\frac{MC+MO}{MN}$=$\frac{2MF}{\sqrt{2}MF}$=$\sqrt{2}$.
点评 本题是反比例函数综合题,考查了图形与坐标特征、反比例函数解析式的求法、正方形的判定与性质、四点共圆以及三角形全等的判定与性质等知识;本题难度较大,综合性强,特别是(2)中,需要通过作辅助线证明正方形和三角形全等才能得出结果.


科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1≥x②}\end{array}\right.$
解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1≥x②}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆A与圆B外离 | B. | 圆B与圆C外离 | C. | 圆A与圆C外离 | D. | 圆A与圆B相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
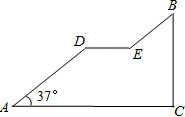 如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.
如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com