
【题目】如图,直线AB与CD相交于点O,OD平分∠BOE,OF⊥OD。
(1)∠AOF与∠EOF相等吗?
(2)写出图中和∠DOE互补的角。
(3)若∠BOE=600,求∠AOD和∠EOF的度数。

【答案】(1)相等;(2) ∠COE,∠BOC,∠AOD;(3)∠AOD=1500,∠EOF=600.
【解析】
试题(1)利用对顶角相等得出∠BOD=∠AOC,OD平分∠BOE,得出∠BOD=∠DOE,在进一步利用等角的余角相等求得∠AOF=∠EOF;
(2)利用补角的意义找出和∠DOE互补的角即可;
(3)利用(1)(2)的结论求得问题即可.
试题解析:解:(1)相等;理由如下:
∵OD平分∠BOE,
∴∠BOD=∠DOE,
又∵∠BOD=∠AOC,
∴∠DOE=∠AOC,
∵OF⊥OD,
∴∠COF=∠DOF=90°,
∴∠AOF=∠EOF;
(2)图中和∠DOE互补的角有∠COE,∠BOC,∠AOD;
(3)∵OD平分∠BOE,
∴∠BOD=∠DOE=![]() ∠BOE=30°,
∠BOE=30°,
∴∠AOD=180°-∠BOD=150°,∠EOF=90°-∠DOE=60°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= ![]() x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= ![]() x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是(
x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ![]() ,1),则点A8的横坐标是 .
,1),则点A8的横坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y= ![]() x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.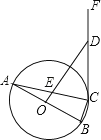
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为5,BC= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,A,B分别是l1,l2上的点,l3和l1,l2分别交于点C,D,P是线段CD上的动点(点P不与C,D重合).
(1)若∠1=150°,∠2=45°,求∠3的度数;
(2)若∠1=α,∠2=β,用α,β表示∠APC+∠BPD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点逆时针旋转度得到的,B1的坐标是;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
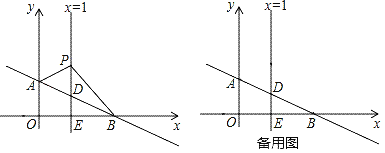
【题目】如图,平面直角坐标系中,直线AB交y轴于点A(0,1),交x轴于点B(3,0).直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,在点D的上方,设P(1,n).
(1)求直线AB的解析式;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为 ![]() ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com