
【题目】如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为 ![]() ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 
【答案】![]() +
+ ![]() ﹣
﹣ ![]()
【解析】解:连接CD′和BC′, ∵∠DAB=60°,
∴∠DAC=∠CAB=30°,
∵∠C′AB′=30°,
∴A、D′、C及A、B、C′分别共线.
∴AC= ![]()
∴扇形ACC′的面积为: ![]() =
= ![]() ,
,
∵AC=AC′,AD′=AB
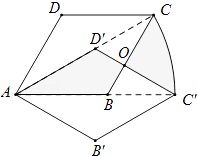
∴在△OCD′和△OC'B中, 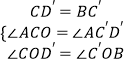
∴△OCD′≌△OC′B(AAS).
∴OB=OD′,CO=C′O
∵∠CBC′=60°,∠BC′O=30°
∴∠COD′=90°
∵CD′=AC﹣AD′= ![]() ﹣1
﹣1
OB+C′O=1
∴在Rt△BOC′中,BO2+(1﹣BO)2=( ![]() ﹣1)2
﹣1)2
解得BO= ![]() ,C′O=
,C′O= ![]() ﹣
﹣ ![]() ,
,
∴S△OC′B= ![]() BOC′O=
BOC′O= ![]() ﹣
﹣ ![]()
∴图中阴影部分的面积为:S扇形ACC′﹣2S△OC′B= ![]() +
+ ![]() ﹣
﹣ ![]() .
.
故答案为: ![]() +
+ ![]() ﹣
﹣ ![]() .
.
根据菱形的性质以及旋转角为30°,连接CD′和BC′,可得A、D′、C及A、B、C′分别共线,求出扇形面积,再根据AAS证得两个小三角形全等,求得其面积,最后根据扇形ACC′的面积﹣两个小的三角形面积即可.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OD平分∠BOE,OF⊥OD。
(1)∠AOF与∠EOF相等吗?
(2)写出图中和∠DOE互补的角。
(3)若∠BOE=600,求∠AOD和∠EOF的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( ) 
A.1:3
B.1:5
C.1:6
D.1:11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠D.说明AB∥CD的理由.
补全下面的说理过程,并在括号内填上适当的理由
解:∵∠1+∠2=180°(已知)
∠2=∠AHB( )
∴ (等量代换)
∴DE∥BF( )
∴∠D=∠ ( )
∵∠ =∠B(等量代换)
∴AB∥CD( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为______.
的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD中,![]() ,
,![]() 绕点A顺时针旋转,它的两边长分别交CB、DC或它们的延长线
绕点A顺时针旋转,它的两边长分别交CB、DC或它们的延长线![]() 于点MN,
于点MN,![]() 于点H.
于点H.
![]() 如图
如图![]() ,当
,当![]() 点A旋转到
点A旋转到![]() 时,请你直接写出AH与AB的数量关系;
时,请你直接写出AH与AB的数量关系;
![]() 如图
如图![]() ,当
,当![]() 绕点A旋转到
绕点A旋转到![]() 时,
时,![]() 中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明.
中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x 度时,应交电费为y 元.具体收费情况如折线图所示,请根据图象回答下列问题:
(1)“基础电价”是____________元 ![]() 度;
度;
(2)求出当x>240 时,y与x的函数表达式;
(3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
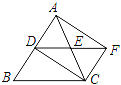
【题目】如图,在△BC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com