
【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y= ![]() x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 . 
【答案】( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() +
+ ![]() ,
, ![]() )
)
【解析】解:如图所示,矩形在这两个位置时就是⊙M的“伴侣矩形”,根据直线l:y= ![]() x﹣3得:OM=
x﹣3得:OM= ![]() ,ON=3,由勾股定理得:MN=
,ON=3,由勾股定理得:MN= ![]() =2
=2 ![]() ,
,
①矩形在x轴下方时,分别过A、D作两轴的垂线AH、DG,
由cos∠ABD=cos∠ONM= ![]() ,∴
,∴ ![]() =
= ![]() ,AB=
,AB= ![]() ,则AD=1,
,则AD=1,
∵DG∥y轴,
∴△MDG∽△MON,
∴ ![]() ,∴
,∴ ![]() ,∴DG=
,∴DG= ![]() ,∴CG=
,∴CG= ![]() +
+ ![]() =
= ![]() ,同理可得:
,同理可得: ![]() ,∴
,∴ ![]() ,∴DH=
,∴DH= ![]() ,∴C(
,∴C( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() );②矩形在x轴上方时,同理可得:C(
);②矩形在x轴上方时,同理可得:C( ![]()
![]() ,
, ![]() );
);
故答案为:( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() +
+ ![]() ,
, ![]() ).
).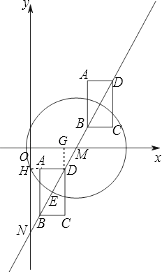
根据“伴侣矩形”的定义可知:圆上的点一定在矩形的对角线交点上,因为只有对角线交点到四个顶点的距离相等,由此画出图形,先求出直线与x轴和y轴两交点的坐标,和矩形的长和宽;
有两种情况:①矩形在x轴下方时,作辅助线构建相似三角形得比例式,分别求出DG和DH的长,从而求出CG的长,根据坐标特点写出点C的坐标;②矩形在x轴上方时,也分别过C、B两点向两坐标轴作垂线,利用平行相似得比例式,求出:C( ![]()
![]() ,
, ![]() ).此题主要考查了圆的综合应用以及相似三角形的性质和矩形等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.同时,正确理解题意准确画出符合条件的矩形是本题的关键,这就需要熟练掌握矩形的对角线的交点到四个顶点的距离相等.
).此题主要考查了圆的综合应用以及相似三角形的性质和矩形等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.同时,正确理解题意准确画出符合条件的矩形是本题的关键,这就需要熟练掌握矩形的对角线的交点到四个顶点的距离相等.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
(1)判断四边形CEGF的形状,并证明你的结论;
(2)若AB=3,BC=9,求线段CE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用数轴解决问题:我们知道,若数轴上点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,则
,则![]() 、
、![]() 两点间的距离记作
两点间的距离记作![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,则
,则![]() = ;
= ;
(2)若数轴上一点![]() 表示的数是
表示的数是![]() ,
,![]() ,则
,则![]() = ;
= ;
(3)若点![]() 表示的数是
表示的数是![]() ,已知
,已知![]() ,点
,点![]() 在
在![]() 的左边,
的左边,![]() ,点
,点![]() 在点
在点![]() 的右边,
的右边,![]() ,点
,点![]() 以每秒
以每秒![]() 的速度向右移动,同时点
的速度向右移动,同时点![]() 、点
、点![]() 分别以每秒
分别以每秒![]() 、
、![]() 的速度向左移动.设移动时间为
的速度向左移动.设移动时间为![]() 秒,那么
秒,那么![]() 是否有最小值?若有,求出最小值并写出此时
是否有最小值?若有,求出最小值并写出此时![]() 的取值范围;若没有,请说明理由.
的取值范围;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a﹣b+c>2.其中正确的结论的个数是( ) 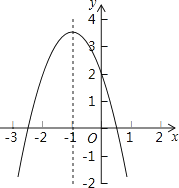
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)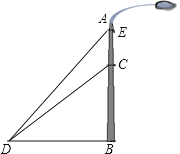
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OD平分∠BOE,OF⊥OD。
(1)∠AOF与∠EOF相等吗?
(2)写出图中和∠DOE互补的角。
(3)若∠BOE=600,求∠AOD和∠EOF的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( ) 
A.1:3
B.1:5
C.1:6
D.1:11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com