
【题目】如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
(1)判断四边形CEGF的形状,并证明你的结论;
(2)若AB=3,BC=9,求线段CE的取值范围.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GFE=∠FEC,
∵图形翻折后点G与点C重合,EF为折线,
∴∠GEF=∠FEC,
∴∠GFE=∠FEG,
∴GF=GE,
∵图形翻折后BC与GE完全重合,
∴BE=EC,
∴GF=EC,
∴四边形CEGF为平行四边形,
∴四边形CEGF为菱形
(2)
解:如图1
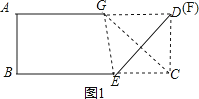 ,
,
当F与D重合时,CE取最小值,
由折叠的性质得CD=DG,∠CDE=∠GDE=45°,
∵∠ECD=90°,
∴∠DEC=45°=∠CDE,
∴CE=CD=DG,
∵DG∥CE,
∴四边形CEGD是矩形,
∴CE=CD=AB=3;
如图2
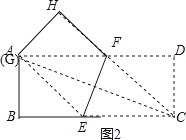 ,
,
当G与A重合时,CE取最大值,
由折叠的性质得AE=CE,
∵∠B=90°,
∴AE2=AB2+BE2,即CE2=32+(9﹣CE)2,
∴CE=5,
∴线段CE的取值范围3≤CE≤5.
【解析】(1)由四边形ABCD是矩形,根据折叠的性质,易证得△EFG是等腰三角形,即可得GF=EC,又由GF∥EC,即可得四边形CEGF为平行四边形,根据邻边相等的平行四边形是菱形,即可得四边形BGEF为菱形;(2)如图1,当G与A重合时,CE取最大值,由折叠的性质得CD=DG,∠CDE=∠GDE=45°,推出四边形CEGD是矩形,根据矩形的性质即可得到CE=CD=AB=3;如图2,当F与D重合时,CE取最小值,由折叠的性质得AE=CE,根据勾股定理即可得到结论.本题考查了翻折变换﹣折叠问题,菱形的判定,线段的最值问题,矩形的性质,勾股定理,正确的作出图形是解题的关键.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】襄阳市文化底蕴深厚,旅游资源丰富,古隆中、习家池、鹿门寺三个景区是人们节假日玩的热点景区,张老师对八(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B、游两个景区;C、游一个景区;D、不到这三个景区游玩.现根据调查结果绘制了不完整的条形统计图和扇形统计图,请结合图中信息解答下列问题: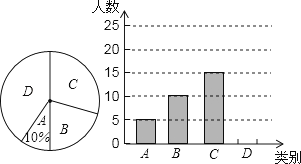
(1)八(1)班共有学生人,在扇形统计图中,表示“B类别”的扇形的圆心角的度数为;
(2)请将条形统计图补充完整;
(3)若张华、李刚两名同学,各自从三个景区中随机选一个作为5月1日游玩的景区,则他们同时选中古隆中的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动.已知点A的速度是1单位长度/秒,点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求请在数轴上标出A、B两点从原点出发运动3秒时的位置;
![]()
(2)若A、B两点在(1)中的位置,数轴上是否存在一点P到点A,点B的距离之和为16,并求出此时点P表示的数;若不存在,请说明理由.
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以10单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商进行商铺促销,广告上写着如下条款:
购买商铺后,都由开发商代为租赁10年,10年期满后再由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:投资者按商铺标价一次性付清铺款,每年可以获得的租金为商铺标价的5%.
方案二:投资者按商铺标价的八五折一次性付清铺款,4年后每年可以获得的租金为商铺标价的5%,但要缴纳租金的10%作为管理费用.
(1)请问:投资者选择哪种购铺方案,10年后所获得的投资收益率更高?为什么?(注:投资收益率=![]() ×100%)
×100%)
(2)(列方程求解)某投资者按方案一购买商铺,因资金周转,决定向银行贷铺款的20%并于一年后付清贷款,已知贷款年利率为5%.那么10年后该投资者获得55.2万元的收益,问铺款是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A在数轴上对应的数为﹣3,点B对应的数为2.
(1)如图1点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣5的解,在数轴上是否存在点P使PA+PB=
x﹣5的解,在数轴上是否存在点P使PA+PB=![]() BC+AB?若存在,求出点P对应的数;若不存在,说明理由;
BC+AB?若存在,求出点P对应的数;若不存在,说明理由;
(2)如图2,若P点是B点右侧一点,PA的中点为M,N为PB的三等分点且靠近于P点,当P在B的右侧运动时,有两个结论:①PM﹣![]() BN的值不变;②
BN的值不变;②![]() BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值
BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= ![]() x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= ![]() x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是(
x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ![]() ,1),则点A8的横坐标是 .
,1),则点A8的横坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y= ![]() x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com