
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )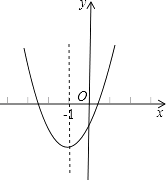
A.(1)(2)(3)(4)
B.(2)(4)(5)
C.(2)(3)(4)
D.(1)(4)(5)
【答案】D
【解析】(1)如图所示,二次函数与x轴有两个交点,所以b2﹣4ac>0,则b2>4ac.故(1)正确;(2)、(3)如图所示,∵抛物线开口向上,所以a>0,抛物线与y轴交点在负半轴上,
∴c<0.
又﹣ ![]() =﹣1,
=﹣1,
∴b=2a>0,
∴abc<0,2a﹣b<0.
故(2)、(3)错误;(4)如图所示,由图象可知当x=1时,y>0,即a+b+c>0.
故(4)正确;(5)由图象可知当x=﹣1时,y<0,即a﹣b+c<0.
故(5)正确.
综上所述,正确的结论是(1)(4)(5).
故答案为:D.
首先依据抛物线的开口方向判断a的正负,然后依据抛物线与y轴的交点判断c的正负,接下来,再根据对称轴及抛物线与x轴交点情况可判断出b的正负以及△的正负.


科目:初中数学 来源: 题型:
【题目】如图,将一个饮料包装盒剪开,铺平,纸样如图所示,包装盒的高为15cm,底面周长为40cm,包装盒底面的长为xcm.
(1)用x表示包装盒底面的宽;
(2)用x表示包装盒的表面积和体积;
(3)若包装盒底面的长为12cm,求包装盒的表面积、体积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的三点A、B、C,点A表示的数为5,点B表示的数为-3,点C到点A、点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
(1)点C在数轴上表示的数是______;
(2)当t=______秒时,点P到达点B处:
(3)用含字母t的代数式表示线段AP=______;点P在数轴上表示的数是______.
(4)当P,C之间的距离为1个单位长度时,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,,ED交BC于点G,BG=4,EF=10,△BEG的面积为4,下列结论:①∠A=∠BED;②△ABC平移的距离是4;③BE=CF;④四边形GCFE的面积为16,正确的有( )

A. ②③B. ①②③C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题:
(1)![]() _____,并把频数分布直方图补充完整;
_____,并把频数分布直方图补充完整;
(2)求扇形![]() 的圆心角度数,成绩众数落在多少分之间;
的圆心角度数,成绩众数落在多少分之间;
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
类型 | 价格 | 进价(元/盏) | 售价(元/盏) |
| 30 | 45 | |
| 50 | 70 | |
(1)若设商场购进![]() 型台灯
型台灯![]() 盏,销售完这批台灯所获利润为
盏,销售完这批台灯所获利润为![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若商场规定![]() 型灯的进货数量不超过
型灯的进货数量不超过![]() 型灯数量的4倍,那么
型灯数量的4倍,那么![]() 型和
型和![]() 型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.
型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.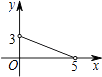
C.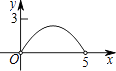
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
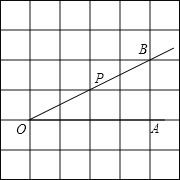
【题目】如图,点P是∠AOB的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C;
(2)过点P画OA的垂线,垂足为H;
(3)线段PH的长度是点P到______的距离,______是点C到直线OB的距离,线段PC、PH、OC这三条线段大小关系是______(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”. 甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.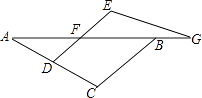
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com