
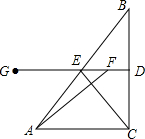
 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在BC的垂直平分线DG上,从D点出发以1cm/秒的速度移动,垂足为D,DG交AB于E,连接CE,设运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在BC的垂直平分线DG上,从D点出发以1cm/秒的速度移动,垂足为D,DG交AB于E,连接CE,设运动时间为t(s).分析 (1)当t=6s时,DF=6cm,根据DG是BC的垂直平分线,∠ACB=90°,可得DF∥AC,DE=$\frac{1}{2}AC$=2cm,再证明AC=EF即可得到四边形ACEF是平行四边形;
(2)①当∠B=30°时,四边形ACEF是菱形,首先证明∠ECA=60°,再证明△AEC是等边三角形,进而可得AC=EC,然后可根据一组邻边相等的平行四边形是菱形得到到结论;
②首先证明四边形ACDF是平行四边形,再由∠ACB=90°可得四边形ACDF是矩形.
解答 (1)证明:当t=6s时,DF=6cm,
∵DG是BC的垂直平分线,∠ACB=90°,
∴DF∥AC,DE=$\frac{1}{2}AC$=2cm,
∴EF=DF-DE=4cm,
∴AC=EF,
∴四边形ACEF是平行四边形;
(2)解:①当∠B=30°时,四边形ACEF是菱形;
∵DG是BC的垂直平分线,
∴BE=EC,
∴∠ECB=∠B=30°,
∴∠ECA=60°,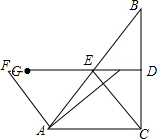
∵DF∥AC,DG是BC的垂直平分线,
∴AE=EB,
∴AE=EC,
∴△AEC是等边三角形,
∴EC=AC,
∴四边形ACEF是菱形,
故答案为:30;
②当t=4s时,四边形ACDF是矩形;
∵动点F从D点出发以1cm/秒的速度移动,
∴DF=4m,
∵AC=4m,DF∥AC,
∴四边形ACDF是平行四边形,
∵∠ACB=90°,
∴四边形ACDF是矩形.
故答案为:4.
点评 此题主要考查了平行四边形、菱形、矩形的判定,关键是掌握特殊四边形的判定定理.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
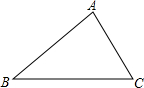 如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )| A. | 作中线AD,再取AD的中点O | |
| B. | 分别作AB、BC的高线,再取此两高线的交点O | |
| C. | 分别作中线AD、BE,再取此两中线的交点O | |
| D. | 分别作∠A、∠B的角平分线,再取此两角平分线的交点O |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com