
分析 (1)②-①得3y=,求出y,把y的值代入①得出关于x的方程3x-3=2,求出x即可.
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)解:原方程组整理得$\left\{\begin{array}{l}{3x-y=2①}\\{3x+2y=11②}\end{array}\right.$,
∵②-①得:3y=9,
解得:y=3,
把y=3代入①得:3x-3=2,
解得:x=$\frac{5}{3}$,
∴方程组的解是:$\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=3}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{5x+2>3(x-1)①}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x②}\end{array}\right.$,
由①得,x>-$\frac{5}{2}$,
由②得,x≤4,
故不等式组的解集为:-$\frac{5}{2}$<x≤4.
在数轴上表示为: .
.
点评 本题考查了解一元一次方程和解一元一次不等式组,解一元一次方程的关键是把二元一次方程组转化成一元一次方程;掌握“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解一元一次不等式组的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
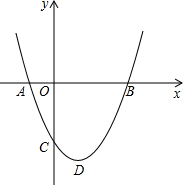 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 进价(元/千克) | 售价(元/千克) | |
| 甲种 | 5 | 8 |
| 乙种 | 9 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
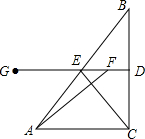 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在BC的垂直平分线DG上,从D点出发以1cm/秒的速度移动,垂足为D,DG交AB于E,连接CE,设运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在BC的垂直平分线DG上,从D点出发以1cm/秒的速度移动,垂足为D,DG交AB于E,连接CE,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
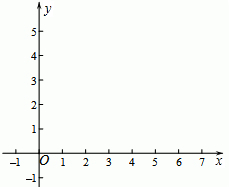 在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD,直线l:y=kx+3.
在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD,直线l:y=kx+3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com