
| 进价(元/千克) | 售价(元/千克) | |
| 甲种 | 5 | 8 |
| 乙种 | 9 | 13 |
分析 利用两种水果每千克的利润表示出总利润,再利用一次函数增减性得出最大值即可.
解答 解:由图表可得:甲种水果每千克利润为:3元,乙种水果每千克利润为:4元,
设总利润为W,由题意可得出:W=3x+4(140-x)=-x+560,
故W随x的增大而减小,则x越小W越大,
因为该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,
∴140-x≤3x,
解得:x≥35,
∴当x=35时,W最大=-35+560=525(元),
故140-35=105(kg).
答:当甲购进35千克,乙种水果105千克时,此时利润最大为525元.
故答案为:35.
点评 主要考查了一次函数的应用,利用一次函数增减性得出函数最值是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
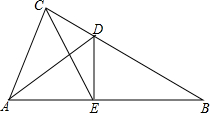 如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.
如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
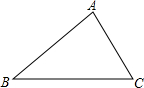 如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )| A. | 作中线AD,再取AD的中点O | |
| B. | 分别作AB、BC的高线,再取此两高线的交点O | |
| C. | 分别作中线AD、BE,再取此两中线的交点O | |
| D. | 分别作∠A、∠B的角平分线,再取此两角平分线的交点O |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com