
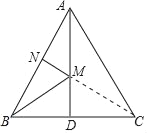
【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=![]() ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )

A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
【答案】A
【解析】
连接CN,与AD交于点M,连接BM,此时BM+MN取得最小值,由AD为∠BAC的角平分线,利用三线合一得到AD⊥BC,且平分BC,可得出BM=CM,由BM+MN=CM+MN=CN,可得出CN的长为最小值,利用等边三角形的性质及勾股定理求出即可.
解:连接CN,与AD交于点M,连接BM,此时BM+MN取得最小值,
由AD为∠BAC的角平分线,利用三线合一得到AD⊥BC,且平分BC,
∴AD为BC的垂直平分线,
∴CM=BM,
∴BM+MN=CM+MN=CN,即最小值为CN的长,
∵△ABC为等边三角形,且AB=2,AN=1,
∴CN为AB边上的中线,
∴CN⊥AB,
在Rt△ACN中,AC=AB=2,AN=1,
根据勾股定理得:CN=![]() =
=![]() .
.
故选:A.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
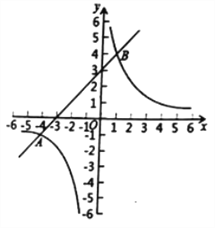
【题目】(9分)已知:如图,在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() 和点和
和点和![]() .
.
(1)求这两个函数的表达式;
(2)观察图象,当![]() 时,直接写出自变量
时,直接写出自变量![]() 的取值范围;
的取值范围;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材的![]() 课题学习
课题学习![]() 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
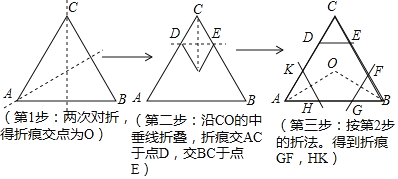
请你根据小明同学的折叠方法,回答以下问题: ![]() 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么![]() ______
______ ![]() 用含a的式子表示
用含a的式子表示![]() ;
;
![]() 根据折叠性质可以知道
根据折叠性质可以知道![]() 的形状为______ 三角形;
的形状为______ 三角形;
![]() 请同学们利用
请同学们利用![]() 、
、![]() 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象上部分点的横坐标x与纵坐标y的对应值如下表:
的图象上部分点的横坐标x与纵坐标y的对应值如下表:
x |
|
| 0 | 1 | 2 |
|
y |
| 0 | 3 | 4 | 3 |
|
那么关于它的图象,下列判断正确的是![]()
A. 开口向上 B. 与x轴的另一个交点是![]()
C. 与y轴交于负半轴 D. 在直线![]() 的左侧部分是下降的
的左侧部分是下降的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的以”垃圾分类 从我做起“的主题知识竞赛活动中,王老师随机抽取了班中参赛的6名学生成绩,若以80分为标准,超过这个分数用正数表示,不足的分数用负数表示,成绩记录如下:-3,+7,-12,+6 , -21 ,+14
(1) 最高分比最低分多多少分?这6名学生平均每人得多少分?
(2) 若规定:成绩高于80分的学生操行分每人加3分,成绩在60~80分的学生操行分每人加2分,成绩在60分以下的学生操行分每人扣1分,那么这6名学生共加操行分多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭![]() 出发,晚上停留在
出发,晚上停留在![]() 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
+5,-8,+10,-12,+6,-18,+5,-2.
(1)![]() 处在岗亭
处在岗亭![]() 的什么方向?距离岗亭
的什么方向?距离岗亭![]() 多远?
多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
![]() 若一元二次方程
若一元二次方程![]() 有一个根是
有一个根是![]() ,则代数式
,则代数式![]() 的值是
的值是![]()
![]() 若
若![]() ,则
,则![]() 是一元二次方程
是一元二次方程![]() 的一个根
的一个根
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有不相等的两个实数根
有不相等的两个实数根
![]() 当m取整数
当m取整数![]() 或1时,关于x的一元二次方程
或1时,关于x的一元二次方程![]() 与
与![]() 的解都是整数.
的解都是整数.
其中正确的有![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
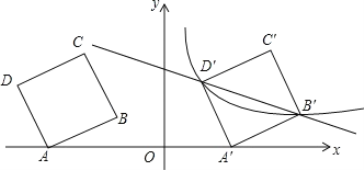
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(-6,0),D(-7,3),点B、C在第二象限内.
(1)点B的坐标 ;
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请求出符合题意的点P、Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com