
【题目】 如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
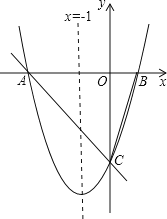
(1)求点B的坐标.
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标.
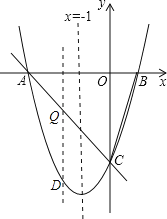
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
【答案】(1)(1,0);(2)①(4,21)或(﹣4,5);②当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.
【解析】
试题分析:(1)由抛物线y=ax2+bx+c的对称轴为直线x=﹣1,交x轴于A、B两点,其中A点的坐标为(﹣3,0),根据二次函数的对称性,即可求得B点的坐标;
(2)①a=1时,先由对称轴为直线x=﹣1,求出b的值,再将B(1,0)代入,求出二次函数的解析式为y=x2+2x﹣3,得到C点坐标,然后设P点坐标为(x,x2+2x﹣3),根据S△POC=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
②先运用待定系数法求出直线AC的解析式为y=﹣x﹣3,再设Q点坐标为(x,﹣x﹣3),则D点坐标为(x,x2+2x﹣3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,
∴A、B两点关于直线x=﹣1对称,
∵点A的坐标为(﹣3,0),
∴点B的坐标为(1,0);
(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,
∴![]() =﹣1,解得b=2.
=﹣1,解得b=2.
将B(1,0)代入y=x2+2x+c,
得1+2+c=0,解得c=﹣3.
则二次函数的解析式为y=x2+2x﹣3,
∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.
设P点坐标为(x,x2+2x﹣3),
∵S△POC=4S△BOC,
∴![]() ×3×|x|=4×
×3×|x|=4×![]() ×3×1,
×3×1,
∴|x|=4,x=±4.
当x=4时,x2+2x﹣3=16+8﹣3=21;
当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.
∴点P的坐标为(4,21)或(﹣4,5);
②设直线AC的解析式为y=kx+t (k≠0)将A(﹣3,0),C(0,﹣3)代入,
得![]() ,解得
,解得![]() ,
,
即直线AC的解析式为y=﹣x﹣3.
设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),
QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.
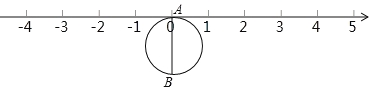
(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C表示的数是__________数(填“无理”或“有理”),这个数是__________;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是__________;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3
①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
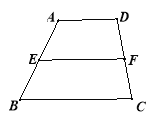
【题目】(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(2)运用三角形中位线的知识解决如下问题:如图,在四边形ABCD中,AD∥BC,E,F分别是AB,CD的中点,求证EF=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=![]() BC,F为CD的中点,连接AF、AE、EF,
BC,F为CD的中点,连接AF、AE、EF,
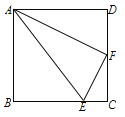
(1)判定△AEF的形状,并说明理由;
(2)设AE的中点为O,判定∠BOF和∠BAF的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
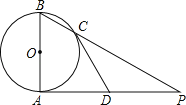
(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定一种新运算“※”,两数a,b通过“※”运算得(a+2)×2﹣b,即a※b=(a+2)×2﹣b,例如:3※5=(3+2)×2﹣5=10﹣5=5.根据上面规定解答下题:
(1)求(7※5)※(﹣3)
(2)7※(﹣3)与(﹣3)※7的值相等吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com