
分析 (1)设购进甲种服装x件,根据题意列出关于x的一元一次不等式,解不等式得出结论;
(2)设每件甲服装应降价为x元,则每件的利润是(40-x)元,售量是(20+$\frac{x}{4}$)件,再根据盈利1200元列方程求解.
解答 解:(1)设购进甲种服装x件,由题意可知:
80x+60(100-x)≤7500,解得:65≤x≤75,
又甲种服装不少于65件,
答:甲种服装最多购进75件;
(2)设每件甲服装应降价为x元,根据题意,得
列方程,得(40-x)(20+$\frac{x}{4}$×8)=1200,
整理,得x2-30x+200=0,
解之,得x1=10,x2=20,
当x=10时,销售量为20+$\frac{x}{4}$×8=40(件).
当x=20时,20+$\frac{x}{4}$×8=60(件).
则每件甲服装应降价10元,此时销售量是40件或每件甲服装应降价20元,此时销售量是60件.
点评 本题考查了一元一次方程的应用,不等式的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意:总利润=每件的利润×售量.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
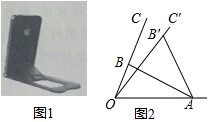 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在OC上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达OC′的位置.已知OA=8cm,AB⊥OC,∠BOA=60°,sin∠B′AO=$\frac{9}{10}$,则点B′到OA的距离$\frac{18\sqrt{3}}{5}$cm.
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在OC上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达OC′的位置.已知OA=8cm,AB⊥OC,∠BOA=60°,sin∠B′AO=$\frac{9}{10}$,则点B′到OA的距离$\frac{18\sqrt{3}}{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
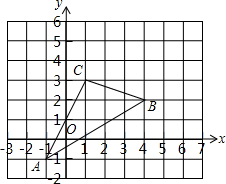 如图,△ABC在直角坐标系中,点A,B,C在格点上.
如图,△ABC在直角坐标系中,点A,B,C在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com