
 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在OC上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达OC′的位置.已知OA=8cm,AB⊥OC,∠BOA=60°,sin∠B′AO=$\frac{9}{10}$,则点B′到OA的距离$\frac{18\sqrt{3}}{5}$cm.
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在OC上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达OC′的位置.已知OA=8cm,AB⊥OC,∠BOA=60°,sin∠B′AO=$\frac{9}{10}$,则点B′到OA的距离$\frac{18\sqrt{3}}{5}$cm. 分析 在Rt△ABO中根据∠AOB=60°、OA=8cm求得AB′=AB=4$\sqrt{3}$cm,在Rt△AB′P中根据B′P=AB′•sin∠B′AO可得答案.
解答 解:∵AB⊥OC,
∴∠ABO=90°,
在Rt△ABO中,∵∠AOB=60°,OA=8cm,
∴AB′=AB=OA•sin∠AOB=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$(cm),
过点B′作B′P⊥OA于点P,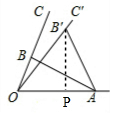
在Rt△AB′P中,∵sin∠B′AO=$\frac{9}{10}$,
∴B′P=AB′•sin∠B′AO=4$\sqrt{3}$×$\frac{9}{10}$=$\frac{18\sqrt{3}}{5}$(cm),
故答案为:$\frac{18\sqrt{3}}{5}$cm
点评 本题主要考查解直角三角形的应用,通过三角函数构建直角三角形是及此类题目的惯用作法,直角三角形中熟练根据已知条件求出所需边长或角的大小是关键.


科目:初中数学 来源: 题型:选择题
| A. | x=3 | B. | x=-1 | C. | x1=3,x2=1 | D. | x1=3,x2=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
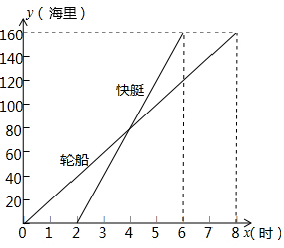 已知A、B两个海港相距180海里.如图表示一艘轮船和一艘快艇沿相同路线从A港出发到B港航行过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).通过计算解答下列问题:
已知A、B两个海港相距180海里.如图表示一艘轮船和一艘快艇沿相同路线从A港出发到B港航行过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).通过计算解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
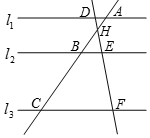 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,则下列式子不正确的是( )
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,则下列式子不正确的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | $\frac{AB}{AC}$=$\frac{DE}{DF}$ | D. | $\frac{AB}{BC}$=$\frac{BE}{CF}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
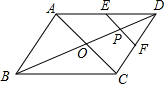 如图,AC、BD相交于点O,且OA=OC=4,OB=OD=6,P是线段BD上一动点,过点P作EF∥AC,与四边形的两条边分别交于点E,F,设BP=x,EF=y,则下列能表示y与x之间函数关系的图象是( )
如图,AC、BD相交于点O,且OA=OC=4,OB=OD=6,P是线段BD上一动点,过点P作EF∥AC,与四边形的两条边分别交于点E,F,设BP=x,EF=y,则下列能表示y与x之间函数关系的图象是( )| A. |  | B. | 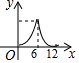 | C. |  | D. | 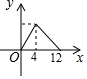 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
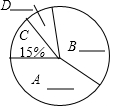 “戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
“戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:| 态度 | A.顾客出面制止 | B.劝说进吸烟室 | C.超市老板出面制止 | D.无所谓 |
| 频数(人数) | 90 | 200 | 30 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com