
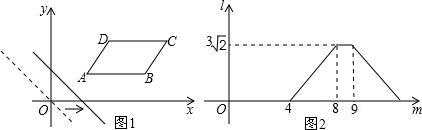
分析 根据平移的特点结合图2,找出相应的线段OE=4,OF=8,DG=3$\sqrt{2}$,OM=9,再利用等腰直角三角形的特点,最后用勾股定理求出AD.
解答 解:①当AB>4时如图1,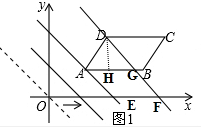
由图可知:OE=4,OF=8,DG=3$\sqrt{2}$,
∴EF=AG=OF-OE=4
∵直线解析式为:y=-x
∴∠AGD=∠EFD=45°
∴△AGD是等腰直角三角形
∴DH=GH=$\frac{\sqrt{2}}{2}$DG=$\frac{\sqrt{2}}{2}$×3$\sqrt{2}$=3,
∴AH=AG-GH=4-3=1,
∴AD=$\sqrt{{DH}^{2}{+AH}^{2}}$=$\sqrt{{3}^{2}{+1}^{2}}$=$\sqrt{10}$;
②当AB=4时,如图2,
由图可知:OI=4,OJ=8,KB=3$\sqrt{2}$,OM=9,
∴IJ=AB=4,IM=AN=5,
∵直线解析式为:y=-x,
∴△KLB是等腰直角三角形,
∴KL=BL=$\frac{\sqrt{2}}{2}$KB=3,
∵AB=4,
∴AL=AB-BL=1,
T同①得,DM=MN,
∴过K作KM∥IM,
∴tan∠DAN=$\frac{KL}{AL}$=3,
∴AM=$\frac{DM}{tan∠DAN}$=$\frac{DM}{3}$,
∴AN=AM+MN=$\frac{4}{3}$DM=5,
∴DM=MN=$\frac{15}{4}$,
∴AM=AN-MN=5-$\frac{15}{4}$=$\frac{5}{4}$,
∴AD=$\sqrt{A{M}^{2}+D{M}^{2}}$=$\frac{5\sqrt{10}}{4}$,
故答案为$\sqrt{10}$或$\frac{5\sqrt{10}}{4}$.
点评 本题是动点问题的函数图象题,主要用平移的特点和勾股定理,三角函数,求出线段的长,解本题的关键是从图②读到信息,OE=4,OF=8,DG=3$\sqrt{2}$,OM=9.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -ab+1 | B. | -ab+b | C. | -a+1 | D. | -a-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
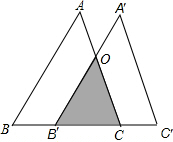 如图,将边长为3$\sqrt{2}$的等边△ABC沿BC方向向右平移得到△A′B′C′,若△ABC与△A′B′C重叠部分面积为2$\sqrt{3}$,则此次平移的距离是( )
如图,将边长为3$\sqrt{2}$的等边△ABC沿BC方向向右平移得到△A′B′C′,若△ABC与△A′B′C重叠部分面积为2$\sqrt{3}$,则此次平移的距离是( )| A. | 3$\sqrt{2}$-2 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
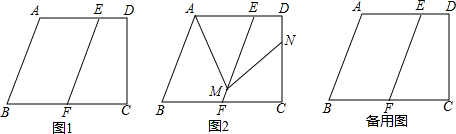
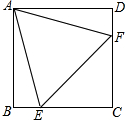 如图,正方形ABCD中,E、F分别是BC,CD边上的点,且△AEF是等边三角形,若BE=1cm,则正方形ABCD的边长是2+$\sqrt{3}$cm.
如图,正方形ABCD中,E、F分别是BC,CD边上的点,且△AEF是等边三角形,若BE=1cm,则正方形ABCD的边长是2+$\sqrt{3}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com