
 某环保器材公司销售一种新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系,每年销售该产品的总开支z(万元)(不含进价成本)与年销售y(万件)存在函数关系z=10y+42.5.
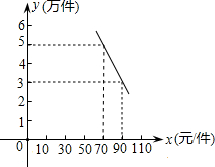
某环保器材公司销售一种新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系,每年销售该产品的总开支z(万元)(不含进价成本)与年销售y(万件)存在函数关系z=10y+42.5.分析 (1)利用待定系数法将点(70,5),(90,3)代入函数解析式求出即可;
(2)利用w=y(x-40)-z进而代入,再利用配方法求出函数最值即可;
(3)根据题意得出结合二次函数性质得出x的取值范围.
解答 解:(1)由题意,设y=kx+b,图象过点(70,5),(90,3)
$\left\{\begin{array}{l}{5=70k+b}\\{3=90k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=12}\end{array}\right.$,
故y与x之间的函数关系式为:y=-$\frac{1}{10}$x+12;
(2)由题意,得:
w=y(x-40)-z
=y(x-40)-(10y+42.5)
=(-$\frac{1}{10}$x+12)×(x-40)-10(-$\frac{1}{10}$x+12)-42.5
=-0.1x2+17x-642.5
=-$\frac{1}{10}$(x-85)2+80,
∴当x=85时,年获利最大值为80万元;
(3)由w=57.5得:-0.1x2+17x-642.5=57.5,
解得:x1=70,x2=100,
结合函数图象的性质可知:70≤x≤100.
点评 此题主要考查了待定系数法求一次函数解析式以及配方法求二次函数最值以及一元二次方程的解法等知识,利用二次函数的性质得出x的取值范围是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
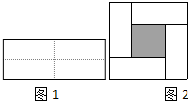 把一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1)
把一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
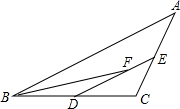 在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com