
【题目】如图,直线y=![]() x+
x+![]() 与双曲线y=
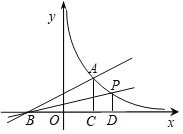
与双曲线y=![]() 在第一象限内的图象交于一点A(1,1),与x负半轴交与点B.点P(m,n)是该双曲线在第一象限内图象上的一点,且P点在A点的右侧,分别过点A、P作x轴的垂线,垂足分别为点C、D,连结PB.则△ABC的面积___△PBD的面积(填“<”、“=”或“>”).
在第一象限内的图象交于一点A(1,1),与x负半轴交与点B.点P(m,n)是该双曲线在第一象限内图象上的一点,且P点在A点的右侧,分别过点A、P作x轴的垂线,垂足分别为点C、D,连结PB.则△ABC的面积___△PBD的面积(填“<”、“=”或“>”).
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
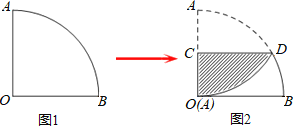
【题目】如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为_____.(答案用根号表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,小颖同学用两块完全一样的透明等腰直角三角板ABC、DEF进行探究活动.
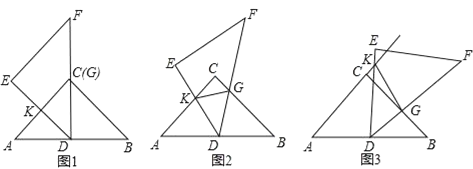
操作:使点D落在线段AB的中点处并使DF过点C(如图1),然后将其绕点D顺时针旋转,直至点E落在AC的延长线上时结束操作,在此过程中,线段DE与AC或其延长线交于点K,线段BC与DF相交于点G(如图2,3).
探究1:在图2中,求证:△ADK∽△BGD.
探究2:在图2中,求证:KD平分∠AKG.
探究3:
①在图3中,KD仍平分∠AKG吗?若平分,请加以证明;若不平分,请说明理由.
②在以上操作过程中,若设AC=BC=8,KG=x,△DKG的面积为y,请求出y与x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下.
(1)补全下表,在所给坐标系中画出函数的图象:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | … |
(2)观察图象,写出该函数两条不同类型的性质;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根,a的取值范围是 .
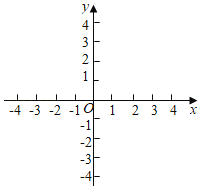
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=9,点C为线段AB上一点,AC=3,点D为平面内一动点,且满足CD=3,连接BD将BD绕点D逆时针旋转90到DE,连接BE、AE,则AE的最大值为 ________。
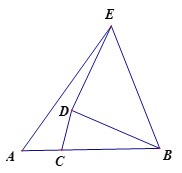
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如右图,O为圆锥的顶点,M为底面圆周上一点,点P在OM上,一只蚂蚁从点P出发绕圆锥侧面爬行回到点P时所经过的最短路径的痕迹如图.若沿OM将圆锥侧面剪开并展平,所得侧面展开图是( )
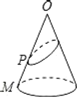
A.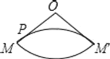 B.
B.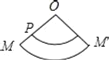
C.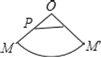 D.
D.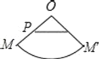
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙![]() 的直径,过点A作⊙
的直径,过点A作⊙![]() 的切线并在其上取一点C,连接OC交⊙
的切线并在其上取一点C,连接OC交⊙![]() 于点D,BD的延长线交AC于E,连接AD.
于点D,BD的延长线交AC于E,连接AD.
(1)求证:![]() ;
;
(2)若AB=2,![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com