
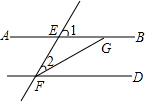
 如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2=
如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2=科目:初中数学 来源: 题型:
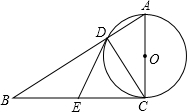 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
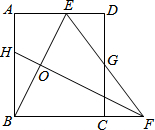 如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次海面搜救行动中,我国的海巡搜救船在某海域的A,B两处探测到C处有疑似飞机黑匣子的脉冲信号,已知A,B两处相距2700米,探测线EC,FC与海平面所在直线GH的夹角分别是32°和45°,试确定疑似脉冲信号所在点C与GH的距离,(精确到0.1米)
在一次海面搜救行动中,我国的海巡搜救船在某海域的A,B两处探测到C处有疑似飞机黑匣子的脉冲信号,已知A,B两处相距2700米,探测线EC,FC与海平面所在直线GH的夹角分别是32°和45°,试确定疑似脉冲信号所在点C与GH的距离,(精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com