
如图所示,某学校拟建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上,菱形的边长AB=4米,∠ABC=60°.设AE=x米(0<x<4),矩形的面积为S米2.
(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,四个三角形内种植黄色花草.已知红色花草的价格为20元/米2,黄色花草的价格为40元/米2.当x为何值时,购买花草所需的总费用最低,并求出最低总费用(结果保留根号).
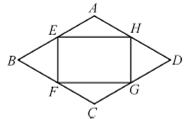
(1)连接AC,BD.AC与EH的交点为M.
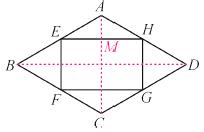
∵花坛为轴对称图形,
∴EH∥BD,EF∥AC.
∴△BEF∽△BAC.
∵∠ABC=60°,∴△ABC,△BEF是等边三角形.
∴EF=B E=AB-AE=4-x.
E=AB-AE=4-x.
在Rt△AEM中,∠AEM=∠ABD=30°,
则EM=AE·cos∠AEM=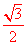 x.
x.
∴EH=2EM= x.
x.
∴S=EH·EF= x·(4-x).
x·(4-x).
即S=- x2+4
x2+4 x.
x.
(2)∵红色花草价格比黄色花草便宜,
∴当矩形面积最大时,购买花草的总费用最低.
又∵S=- x2+4
x2+4 x=-
x=- (x-2)2+4
(x-2)2+4 ,
,
∴当x=2时,S最大=4 .易得S四边形ABCD=8
.易得S四边形ABCD=8 .
.
此时四个三角形的面积为8 -4
-4 =4
=4 (米2).
(米2).
∴最低总费用为:20×4 +40×4
+40×4 =240
=240 (元).
(元).
答:当x=2时,购买花草所需的总费用最低,最低总费用是240 元.
元.


科目:初中数学 来源: 题型:
已知点A(a-2b,2-4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( ) A.(-3,7) B.(-1,7) C.(-4,10) D.(0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
2013年 5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系y=-
5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系y=-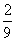 x2+
x2+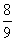 x+
x+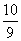 ,则羽毛球飞出的水平距离为 米.
,则羽毛球飞出的水平距离为 米.

查看答案和解析>>
科目:初中数学 来源: 题型:
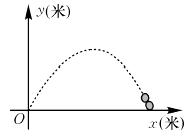
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末考试数学试卷(解析版) 题型:解答题
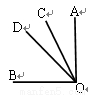
(5分)如图,已知∠AOB=90°,∠BOC:∠AOC= 2 :1 ,OD是∠AOB的平分线,求∠COD的度数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末考试数学试卷(解析版) 题型:选择题
“聪”和“明”是一对好朋友,聪说:“学数学就像玩游戏,一旦掌握了规则,就很容易了!”明说:“那我考考你,若规定:x◎y = x + |y| , 如1 ◎(-2)= 1 + |-2|=1+2=3,那么(-2)◎ 1 =( )?”聪很快说出了答案,你也试试吧!
A.﹣3 B.﹣1 C.1 D.3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级下学期期始考试数学试卷(解析版) 题型:解答题
(本题10分)为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com