
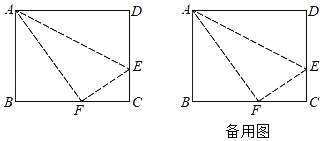
【题目】如图,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F处
(1)求CE的长;
(2)在(1)的条件下,BC边上是否存在一点P,使得PA+PE值最小?若存在,请求出最小值:若不存在,请说明理由.
【答案】(1)3;(2)存在,![]() .
.
【解析】
(1)先判断出AF=AD=8,进而利用勾股定理求出BF=6,最后在Rt△ECF,利用勾股定理,即可得出结论;
(2)先作出点E关于BC的对称点E,进而求出DE',再利用勾股定理即可得出结论.
解:(1)长方形ABCD中,AB=8,BC=10,
∴∠B=∠BCD=90°,CD=AB=8,AD=BC=10,
由折叠知,EF=DE,AF=AD=8,
在Rt△ABF中,根据勾股定理得,BF=![]() =6,
=6,
∴CF=BC﹣BF=4,
设CE=x,则EF=DE=CD﹣CE=8﹣x,
在Rt△ECF中,根据勾股定理得,CF2+CE2=EF2,
∴16+x2=(8﹣x)2,
∴x=3,
∴CE=3;
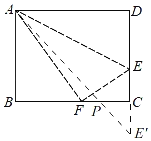
(2)如图,延长EC至E'使CE'=CE=3,连接AE'交BC于P,
此时,PA+PE最小,最小值为AE',
∵CD=8,
∴DE'=CD+CE'=8+3=11,
在Rt△ADE'中,根据勾股定理得,AE'=![]() =
=![]() .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 有两条边相等的两个等腰三角形全等
B. 两腰对应相等的两个等腰三角形全等
C. 两角对应相等的两个等腰三角形全等
D. 一边对应相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一大重要研究成果.如图所示的三角形数表,称“杨辉三角”.具体法则:两侧的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律:
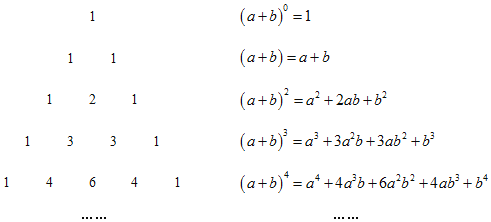
(1)根据上面的规律,写出(a+b)5的展开式;
(2)利用上面的规律计算:(﹣3)4+4×(﹣3)3×2+6×(﹣3)2×22+4×(﹣3)×23+24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,若每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,求:
(1)每千克应涨价多少元?
(2)该水果月销售(按每月30天)是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD,AE分别是△ABC的高和中线,AB=3cm,AC=4cm,BC=5cm,∠CAB=90°,求:
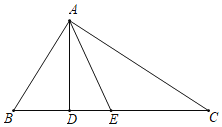
(1)AD的长;
(2)△ACE和△ABE的周长的差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)作侧面和底面,加工成如图2所示的竖式和横式两种无盖的长方体纸箱.(加工时接缝材料不计)


图1 图2
(1)若该厂仓库里有1000张正方形纸板和2000张长方形纸板。问竖式和横式纸箱各加工多少个,恰好将库存的两种纸板全部用完?
(2)该工厂原计划用若干天加工纸箱2400个,后来由于对方急需要货,实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务,问原计划每天加工纸箱多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com