
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)作侧面和底面,加工成如图2所示的竖式和横式两种无盖的长方体纸箱.(加工时接缝材料不计)


图1 图2
(1)若该厂仓库里有1000张正方形纸板和2000张长方形纸板。问竖式和横式纸箱各加工多少个,恰好将库存的两种纸板全部用完?
(2)该工厂原计划用若干天加工纸箱2400个,后来由于对方急需要货,实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务,问原计划每天加工纸箱多少个?
【答案】(1)加工竖式纸盒200个,横式纸盒400个;(2)原计划每天加工纸箱400个
【解析】
(1)设加工竖式纸箱![]() 个,横式纸箱
个,横式纸箱![]() 个,根据竖式纸箱需要4张长方形纸板,1张正方形纸板,横式纸箱需要3张长方形纸板,2张正方形纸板列出方程组,然后求解方程组即可;
个,根据竖式纸箱需要4张长方形纸板,1张正方形纸板,横式纸箱需要3张长方形纸板,2张正方形纸板列出方程组,然后求解方程组即可;
(2)设原计划每天加工纸箱![]() 个,根据“实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务”列出关于a的分式方程,然后求解方程验根即可.
个,根据“实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务”列出关于a的分式方程,然后求解方程验根即可.
解:(1)设加工竖式纸箱![]() 个,横式纸箱
个,横式纸箱![]() 个,
个,
由题意,得![]() ,
,
解得![]() ,
,
答:加工竖式纸盒200个,横式纸盒400个;
(2)设原计划每天加工纸箱![]() 个,
个,
由题意,得![]() ,
,
解得![]() ,
,
经检验:![]() 是所列方程的根,且符合题意.
是所列方程的根,且符合题意.
答:原计划每天加工纸箱400个.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A(a,6),B(4,b),
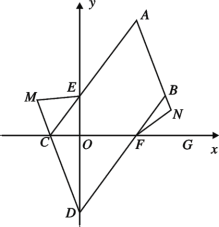
(1)若 a,b 满足 (a b 5)2 ![]() 0 ,
0 ,
①求点 A,B 的坐标;
②点 D 在第一象限,且点 D 在直线 AB 上,作 DC⊥x 轴于点 C,延长 DC 到 P 使 得 PC=DC,若△PAB 的面积为 10,求 P 点的坐标;
(2)如图,将线段 AB 平移到 CD,且点 C 在 x 轴负半轴上,点 D 在 y 轴负半轴上, 连接 AC 交 y 轴于点 E,连接 BD 交 x 轴于点 F,点 M 在 DC 延长线上,连 EM,3∠MEC+∠CEO=180°,点 N 在 AB 延长线上,点 G 在 OF 延长线上,∠NFG= 2∠NFB,请探究∠EMC 和∠BNF 的数量关系,给出结论并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
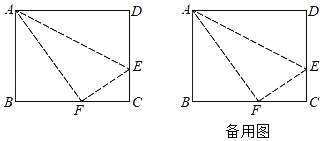
【题目】如图,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F处
(1)求CE的长;
(2)在(1)的条件下,BC边上是否存在一点P,使得PA+PE值最小?若存在,请求出最小值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
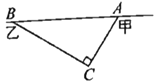
【题目】在甲村至乙村的公路上有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站![]() 的距离为400米,且
的距离为400米,且![]() ,如图所示为了安全起见,爆破点
,如图所示为了安全起见,爆破点![]() 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路![]() 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.2万元,乙队每天的施工费用为5.8万元.工程预算的施工费用为501万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() .
.
(![]() )把
)把![]() 绕点
绕点![]() 按顺时针方向旋转,得
按顺时针方向旋转,得![]() ,
, ![]() 交
交![]() 于点
于点![]() .
.
①若![]() ,旋转角为
,旋转角为![]() ,求
,求![]() 的长.
的长.
②若点![]() 经过的路径与
经过的路径与![]() ,
, ![]() 所围图形的面积与
所围图形的面积与![]() 面积的比值是
面积的比值是![]() ,求
,求![]() 的度数.
的度数.
(![]() )点
)点![]() 在边
在边![]() 上,
上, ![]() ,把
,把![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 度后,如果点
度后,如果点![]() 恰好落在初始
恰好落在初始![]() 的边上,求
的边上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形△ABC,BC边上的高恰好等于BC边长的一半,则∠BAC的度数是( )
A.90°B.90°或75°
C.90°或 75°或15°D.90°或75°或15°或60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com