
【题目】在平面直角坐标系中,点 A(a,6),B(4,b),
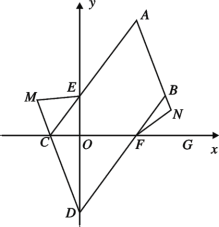
(1)若 a,b 满足 (a b 5)2 ![]() 0 ,
0 ,
①求点 A,B 的坐标;
②点 D 在第一象限,且点 D 在直线 AB 上,作 DC⊥x 轴于点 C,延长 DC 到 P 使 得 PC=DC,若△PAB 的面积为 10,求 P 点的坐标;
(2)如图,将线段 AB 平移到 CD,且点 C 在 x 轴负半轴上,点 D 在 y 轴负半轴上, 连接 AC 交 y 轴于点 E,连接 BD 交 x 轴于点 F,点 M 在 DC 延长线上,连 EM,3∠MEC+∠CEO=180°,点 N 在 AB 延长线上,点 G 在 OF 延长线上,∠NFG= 2∠NFB,请探究∠EMC 和∠BNF 的数量关系,给出结论并说明理由.
【答案】(1)①A(2,6),B(4,3).②P(![]() ,-5).(2)∠BNF-∠EMC=30°,理由见解析.
,-5).(2)∠BNF-∠EMC=30°,理由见解析.
【解析】
(1)①利用非负数的性质构建方程组解决问题即可.
②由题意AB的解析式为y=-![]() x+9,设D(m,-
x+9,设D(m,-![]() m+9),利用三角形的面积,构建方程解决问题即可.
m+9),利用三角形的面积,构建方程解决问题即可.
(2)结论:∠BNF-∠EMC=30°.设∠MEC=α,∠BFN=β,首先证明α-β=30°,再利用平行四边形的性质,三角形的外角的性质解决问题即可.
(1)①∵(a+b-5)2+|2a-b-1|=0,
又∵(a+b-5)2≥0,|2a-b-1|≥0,
∴![]() ,
,
∴![]() ,
,
∴A(2,6),B(4,3).
②如图1中,

∵A(2,6),B(4,3),
∴直线AB的解析式为y=-![]() x+9,设D(m,-
x+9,设D(m,-![]() m+9),
m+9),
∵CD=PC,
∴PD=-3m+18,
∵S△PAB=10,
∴![]() ×PD×2=10,
×PD×2=10,
∴-3m+18=10,
∴m=![]() ,
,
∴D(![]() ,5),
,5),
∴P(![]() ,-5).
,-5).
(2)结论:∠BNF-∠EMC=30°.
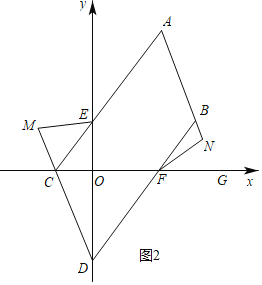
理由:设∠MEC=α,∠BFN=β,
∵3∠MEC+∠CEO=180°,∠AEO+∠CEO=180°,
∴∠AEO=3α,
∵∠NFG=2∠BFN,
∴∠NFG=2β,∠OFD=∠BFG=3β,
∵AB=CD,AB∥CD,
∴四边形ABDC是平行四边形,
∴AC∥BD,∠ACD=∠ABD,
∴∠BDE=180°-∠AEO=180°-3α,
∵∠BDE+∠OFD=90°,
∴180°-3α+3β=90°,
∴α-β=30°,
∵∠ACD=∠EMC+∠MEC,∠ABD=∠BFN+∠BNF,
∴∠EMC+α=∠BNF+β,
∴∠BNF-∠EMC=α-β=30°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
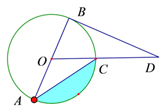
【题目】如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4.
(1) 求∠BAC的大小;
(2) 求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 有两条边相等的两个等腰三角形全等
B. 两腰对应相等的两个等腰三角形全等
C. 两角对应相等的两个等腰三角形全等
D. 一边对应相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选
取该校100名学生进行调查,要求每名学生只选出一类自己最喜爱的节目,根据调查结果 绘制了不完整的条形图和扇形统计图(如图),
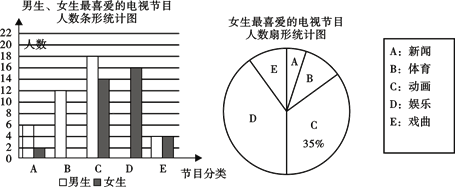
根据图中提供的信息,解答下列问题:
(1)这次抽样调查的女生人数是_______人;
(2)扇形统计图中, “A”组对应的圆心角度数为_______,并将条形图中补充完整;
(3)若该校有 1800 名学生,试估计全校最喜欢新闻和戏曲的学生一共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一大重要研究成果.如图所示的三角形数表,称“杨辉三角”.具体法则:两侧的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律:
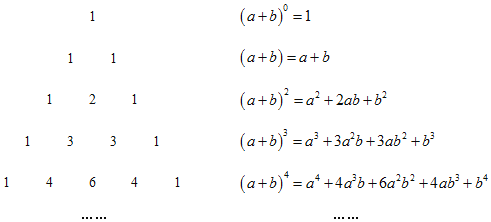
(1)根据上面的规律,写出(a+b)5的展开式;
(2)利用上面的规律计算:(﹣3)4+4×(﹣3)3×2+6×(﹣3)2×22+4×(﹣3)×23+24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)作侧面和底面,加工成如图2所示的竖式和横式两种无盖的长方体纸箱.(加工时接缝材料不计)


图1 图2
(1)若该厂仓库里有1000张正方形纸板和2000张长方形纸板。问竖式和横式纸箱各加工多少个,恰好将库存的两种纸板全部用完?
(2)该工厂原计划用若干天加工纸箱2400个,后来由于对方急需要货,实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务,问原计划每天加工纸箱多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com