
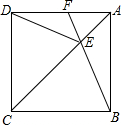
 如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.分析 (1)根据正方形的性质得出BC=DC,∠BCE=∠DCE=45°,根据SAS推出即可;
(2)根据全等求出∠DEC=∠BEC=70°,根据三角形内角和定理求出∠FBC,根据平行线的性质求出即可.
解答 (1)证明:∵正方形ABCD中,E为对角线AC上一点,
∴BC=DC,∠BCE=∠DCE=45°,
在△BCE和△DCE中
$\left\{\begin{array}{l}{CE=CE}\\{∠BCE=∠DCE}\\{BC=DC}\end{array}\right.$
∴△BCE≌△DCE(SAS);
(2)解:由全等可知,∠BEC=∠DEC=$\frac{1}{2}$∠DEB=$\frac{1}{2}$×140°=70°,
∵在△BCE中,∠CBE=180°-70°-45°=65°,
∴在正方形ABCD中,AD∥BC,有∠AFE=∠CBE=65°.
点评 本题考查了正方形的性质,全等三角形的性质和判定,三角形内角和定理,平行线的性质的应用,解此题的关键是求出△BCE≌△DCE,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播放广告这一事件是随机事件 | |
| B. | 要了解小红一家三口的身高,适合采用抽样调查 | |
| C. | 方差越大,数据的波动越大 | |
| D. | 样本中个本的数目称为样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 极差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com