
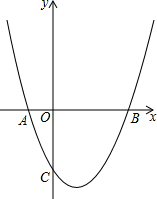
 已知二次函数y=ax2+bx+c(a≠0)的图象与坐标轴交点的坐标分别为A(-1,0),B(3,0),C(0,-3).
已知二次函数y=ax2+bx+c(a≠0)的图象与坐标轴交点的坐标分别为A(-1,0),B(3,0),C(0,-3).分析 (1)设抛物线的解析式为y=a(x-x1)(x-x2),再把A(-1,0),B(3,0),C(0,-3)代入即可得出此函数的解析式;
(2)根据a的符号判断抛物线的开口方向、由顶点公式得出对称轴及顶点坐标;
(3)由题意把函数转化为不等式,得x2-2x-3>0,从而求出x的取值范围.
解答 解:(1)设抛物线的解析式为y=a(x-x1)(x-x2),
把A(-1,0),B(3,0),C(0,-3)代入得a(0+1)(0-3)=-3,
解得a=1,
∴此函数的解析式y=(x+1)(x-3)即y=x2-2x-3;
(2)∵a=1>0,
∴抛物线的开口向上,
对称轴为直线x=-$\frac{b}{2a}$=1,
$\frac{4ac-{b}^{2}}{4a}$=$\frac{-12-4}{4}$=-4,
顶点坐标(1,-4);
(3)∵y<0,即图象在x轴的下方,
∴由图象可知:当-1<x<3时,y<0.
点评 本题考查了二次函数的性质,以及用待定系数法求二次函数的解析式,求抛物线的顶点坐标的方法,是中考的常见题型.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x2+1=0 | B. | x2-2x+1=0 | C. | x2+x+1=0 | D. | x2+2x-1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
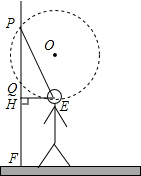 如图,墙壁上的展品最高点与地面的距离PF=3.2m,最低点与地面的距离QF=2m,观赏者的眼睛E距地面1.6m,经验表明,当水平视线EH与过P,Q,E点的圆相切于点E时,视角最大,站在此处观赏最理想,求此时点E到墙壁的距离EH.
如图,墙壁上的展品最高点与地面的距离PF=3.2m,最低点与地面的距离QF=2m,观赏者的眼睛E距地面1.6m,经验表明,当水平视线EH与过P,Q,E点的圆相切于点E时,视角最大,站在此处观赏最理想,求此时点E到墙壁的距离EH.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 0或2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com