
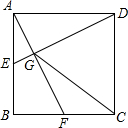
 如图,在正方形ABCD中,E,F分别为AB,BC的中点,AF,DE相交于点G,连接CG,则tan∠DGC=2.
如图,在正方形ABCD中,E,F分别为AB,BC的中点,AF,DE相交于点G,连接CG,则tan∠DGC=2. 分析 根据正方形的性质可得AB=AD,∠B=∠BAD=90°,再求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠AED=∠BFA,再求出∠AGE=90°,从而得到AF⊥DE,取AD的中点H,连接CH,再判断出CH垂直平分DG,根据线段垂直平分线上的点到两端点的距离相等可得CD=CG,根据等边对等角可得∠CGD=∠CDG,再求出∠CGD=∠AED,设正方形的边长为2a,求出AE,根据锐角的正切等于对边和邻边的比即可得出结果.
解答 解:如图,在正方形ABCD中,AB=AD,∠B=∠BAD=90°,
∵E、F分别为AB、BC边的中点,
∴AE=BF,
在△ABF和△DAE中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠B=∠BAD}&{\;}\\{AE=BF}&{\;}\end{array}\right.$,
∴△ABF≌△DAE(SAS),
∴∠AED=∠BFA,
∵∠BAF+∠AED=∠BAF+∠BFA=90°,
∴∠AGE=90°,
∴AF⊥DE,
取AD的中点H,连接CH,
∵H是AD的中点,∴CH∥AF,
设CH与DG相交于点M,则MH是三角形ADG的中位线,
∴DM=GM,
∴CH垂直平分DG,
∴CD=CG,
∴∠CGD=∠CDG,
∵AB∥CD,
∴∠CGD=∠AED,
设正方形的边长为2a,则AE=a,
∴tan∠DGC=∠AED=$\frac{2a}{a}$=2;
故答案为:2.
点评 本题考查了正方形的性质、全等三角形的判定与性质、勾股定理、锐角三角函数的定义、线段垂直平分线的性质;熟记性质并作辅助线把∠DGC转化为∠AED是解题的关键.


科目:初中数学 来源: 题型:填空题
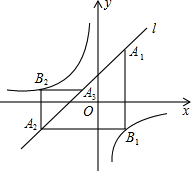 如图,在平面直角坐标系xOy中,已知l:直线y=x+1,双曲线y=-$\frac{1}{x}$,在l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,请继续操作并探究:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,这样依次得到直线l上的点A1,A2,A3,…An,….点An的横坐标为an,若a1=1,则a2015=-2.
如图,在平面直角坐标系xOy中,已知l:直线y=x+1,双曲线y=-$\frac{1}{x}$,在l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,请继续操作并探究:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,这样依次得到直线l上的点A1,A2,A3,…An,….点An的横坐标为an,若a1=1,则a2015=-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
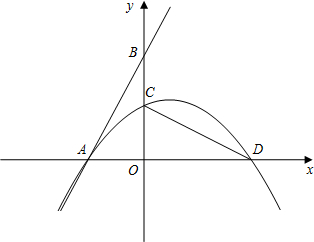 如图,在平面直角坐标系中,直线$y=-\frac{1}{2}{x^2}+\frac{1}{2}x+1$交Rt△COD轴于点A,交y轴于点B,将△AOB绕原点O顺时针旋转90°后得到△COD,抛物线经过点A、C、D.
如图,在平面直角坐标系中,直线$y=-\frac{1}{2}{x^2}+\frac{1}{2}x+1$交Rt△COD轴于点A,交y轴于点B,将△AOB绕原点O顺时针旋转90°后得到△COD,抛物线经过点A、C、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
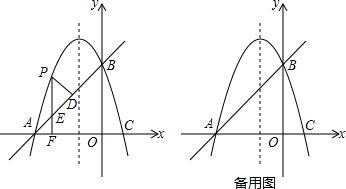
 如图,A(4,0),B(0,4)两点,P在BA延长线上,△OPE为等腰直角三角形,F为PE的中点,OF交AB于M.
如图,A(4,0),B(0,4)两点,P在BA延长线上,△OPE为等腰直角三角形,F为PE的中点,OF交AB于M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com