
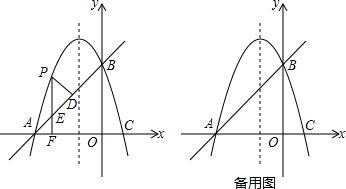
ЗжЮі ЃЈ1ЃЉАбЕуAЁЂCЕФзјБъДњШыХзЮяЯпНтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪННтД№МДПЩЃЛ
ЃЈ2ЃЉЂйИљОнЕуAЁЂBЕФзјБъЧѓГіOA=OBЃЌДгЖјЕУЕНЁїAOBЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУЁЯBAO=45ЁуЃЌШЛКѓЧѓГіЁїPEDЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌPDдНДѓЃЌЁїPDEЕФжмГЄзюДѓЃЌдйХаЖЯГіЕБгыжБЯпABЦНааЕФжБЯпгыХзЮяЯпжЛгавЛИіНЛЕуЪБЃЌPDзюДѓЃЌдйЧѓГіжБЯпABЕФНтЮіЪНЮЊy=x+3ЃЌЩшгыABЦНааЕФжБЯпНтЮіЪНЮЊy=x+mЃЌгыХзЮяЯпНтЮіЪНСЊСЂЯћЕєyЃЌЕУЕНЙигкxЕФвЛдЊЖўДЮЗНГЬЃЌРћгУИљЕФХаБ№ЪНЁї=0СаЪНЧѓГіmЕФжЕЃЌдйЧѓГіxЁЂyЕФжЕЃЌДгЖјЕУЕНЕуPЕФзјБъЃЛ
ЂкЯШШЗЖЈГіХзЮяЯпЕФЖдГЦжсЃЌШЛКѓЃЈiЃЉЗжЕуMдкЖдГЦжсЩЯЪБЃЌЙ§ЕуPзїPQЁЭЖдГЦжсгкQЃЌИљОнЭЌНЧЕФгрНЧЯрЕШЧѓГіЁЯAPF=ЁЯQPMЃЌдйРћгУЁАНЧНЧБпЁБжЄУїЁїAPFКЭЁїMPQШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУPF=PQЃЌЩшЕуPЕФКсзјБъЮЊnЃЌБэЪОГіPQЕФГЄЃЌМДPFЃЌШЛКѓДњШыХзЮяЯпНтЮіЪНМЦЫуМДПЩЕУНтЃЛЃЈiiЃЉЕуNдкЖдГЦжсЩЯЪБЃЌЭЌРэЧѓГіЁїAPFКЭЁїANQШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУPF=AQЃЌИљОнЕуAЕФзјБъЧѓГіЕуPЕФзнзјБъЃЌдйДњШыХзЮяЯпНтЮіЪНЧѓГіКсзјБъЃЌМДПЩЕУЕНЕуPЕФзјБъЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпХзЮяЯпy=ax2+bx+3ОЙ§ЕуAЃЈ-3ЃЌ0ЃЉЃЌCЃЈ1ЃЌ0ЃЉЃЌ
Ёр$\left\{\begin{array}{l}{9a-3b+3=0}\\{a+b+3=0}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$ЃЌ
ЫљвдЃЌХзЮяЯпЕФНтЮіЪНЮЊy=-x2-2x+3ЃЛ
ЃЈ2ЃЉЂйЁпAЃЈ-3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌ
ЁрOA=OB=3ЃЌ
ЁрЁїAOBЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯBAO=45ЁуЃЌ
ЁпPFЁЭxжсЃЌ
ЁрЁЯAEF=90Ёу-45Ёу=45ЁуЃЌ
гжЁпPDЁЭABЃЌ
ЁрЁїPDEЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPDдНДѓЃЌЁїPDEЕФжмГЄдНДѓЃЌ
взЕУжБЯпABЕФНтЮіЪНЮЊy=x+3ЃЌ
ЩшгыABЦНааЕФжБЯпНтЮіЪНЮЊy=x+mЃЌ
СЊСЂ$\left\{\begin{array}{l}{y=x+m}\\{y=-{x}^{2}-2x+3}\end{array}\right.$ЃЌ
ЯћЕєyЕУЃЌx2+3x+m-3=0ЃЌ
ЕБЁї=32-4ЁС1ЁСЃЈm-3ЃЉ=0ЃЌ
МДm=$\frac{21}{4}$ЪБЃЌжБЯпгыХзЮяЯпжЛгавЛИіНЛЕуЃЌPDзюГЄЃЌ
ДЫЪБx=-$\frac{3}{2}$ЃЌy=-$\frac{3}{2}$+$\frac{21}{4}$=$\frac{15}{4}$ЃЌ
ЁрЕуPЃЈ-$\frac{3}{2}$ЃЌ$\frac{15}{4}$ЃЉЪБЃЌЁїPDEЕФжмГЄзюДѓЃЛ
ЂкХзЮяЯпy=-x2-2x+3ЕФЖдГЦжсЮЊжБЯпx=-$\frac{-2}{2ЁСЃЈ-1ЃЉ}$=-1ЃЌ
ЃЈiЃЉШчЭМ1ЃЌЕуMдкЖдГЦжсЩЯЪБЃЌЙ§ЕуPзїPQЁЭЖдГЦжсгкQЃЌ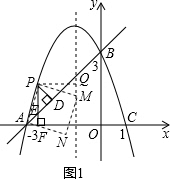
дке§ЗНаЮAPMNжаЃЌAP=PMЃЌЁЯAPM=90ЁуЃЌ
ЁрЁЯAPF+ЁЯFPM=90ЁуЃЌЁЯQPM+ЁЯFPM=90ЁуЃЌ
ЁрЁЯAPF=ЁЯQPMЃЌ
ЁпдкЁїAPFКЭЁїMPQжаЃЌ
$\left\{\begin{array}{l}{ЁЯAPF=ЁЯQPM}\\{ЁЯAFP=ЁЯMQP=90Ёу}\\{AP=PM}\end{array}\right.$ЃЌ
ЁрЁїAPFЁеЁїMPQЃЈAASЃЉЃЌ
ЁрPF=PQЃЌ
ЩшЕуPЕФКсзјБъЮЊnЃЈnЃМ0ЃЉЃЌдђPQ=-1-nЃЌ
МДPF=-1-nЃЌ
ЁрЕуPЕФзјБъЮЊЃЈnЃЌ-1-nЃЉЃЌ
ЁпЕуPдкХзЮяЯпy=-x2-2x+3ЩЯЃЌ
Ёр-n2-2n+3=-1-nЃЌ
ећРэЕУЃЌn2+n-4=0ЃЌ
НтЕУn1=$\frac{-1+\sqrt{17}}{2}$ЃЈЩсШЅЃЉЃЌn2=$\frac{-1-\sqrt{17}}{2}$ЃЌ
-1-n=-1-$\frac{-1-\sqrt{17}}{2}$=$\frac{-1+\sqrt{17}}{2}$ЃЌ
ЫљвдЃЌЕуPЕФзјБъЮЊЃЈ$\frac{-1-\sqrt{17}}{2}$ЃЌ$\frac{-1+\sqrt{17}}{2}$ЃЉЃЛ
ЃЈiiЃЉШчЭМ2ЃЌЕуNдкЖдГЦжсЩЯЪБЃЌЩшХзЮяЯпЖдГЦжсгыxжсНЛгкЕуQЃЌ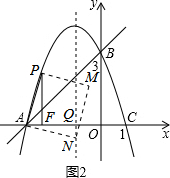
ЁпЁЯPAF+ЁЯFPA=90ЁуЃЌЁЯPAF+ЁЯQAN=90ЁуЃЌ
ЁрЁЯFPA=ЁЯQANЃЌ
гжЁпЁЯPFA=ЁЯAQN=90ЁуЃЌPA=ANЃЌ
ЁрЁїAPFЁеЁїNAQЃЌ
ЁрPF=AQЃЌ
ЩшЕуPзјБъЮЊPЃЈxЃЌ-x2-2x+3ЃЉЃЌ
дђга-x2-2x+3=-1-ЃЈ-3ЃЉ=2ЃЌ
НтЕУx=$\sqrt{2}$-1ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЛђx=-$\sqrt{2}$-1ЃЌ
ДЫЪБЕуPзјБъЮЊЃЈ-$\sqrt{2}$-1ЃЌ2ЃЉЃЎ
злЩЯЫљЪіЃЌЕБЖЅЕуMЧЁКУТфдкХзЮяЯпЖдГЦжсЩЯЪБЃЌЕуPзјБъЮЊЃЈ$\frac{-1-\sqrt{17}}{2}$ЃЌ$\frac{-1+\sqrt{17}}{2}$ЃЉЃЌЕБЖЅЕуNЧЁКУТфдкХзЮяЯпЖдГЦжсЩЯЪБЃЌЕуPЕФзјБъЮЊЃЈ-$\sqrt{2}$-1ЃЌ2ЃЉЃЎ
ЕуЦР БОЬтЪЧЖўДЮКЏЪ§злКЯЬтаЭЃЌжївЊПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪНЃЌЕШбќжБНЧШ§НЧаЮЕФХаЖЈгыаджЪЃЌе§ЗНаЮЕФаджЪЃЌШЋЕШШ§НЧаЮЕФХаЖЈгыаджЪЃЌХзЮяЯпЩЯЕуЕФзјБъЬиеїЃЌЃЈ2ЃЉШЗЖЈГіЁїPDEЪЧЕШбќжБНЧШ§НЧаЮЃЌДгЖјХаЖЯГіЕуPЮЊЦНаагкABЕФжБЯпгыХзЮяЯпжЛгавЛИіНЛЕуЪБЕФЮЛжУЪЧНтЬтЕФЙиМќЃЌЃЈ3ЃЉИљОнШЋЕШШ§НЧаЮЕФаджЪгУЕуPЕФКсзјБъБэЪОГізнзјБъЛђгУзнзјБъЧѓГіКсзјБъЪЧНтЬтЕФЙиМќЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | -2 | BЃЎ | -1 | CЃЎ | 0 | DЃЎ | 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
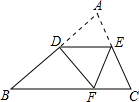 ШчЭМЃЌDЪЧABБпЩЯЕФжаЕуЃЌDEЁЮBCЃЌНЋЁїABCбиЙ§DЕФжБЯпелЕўЃЌЪЙЕуAТфдкBCЩЯFДІЃЌ
ШчЭМЃЌDЪЧABБпЩЯЕФжаЕуЃЌDEЁЮBCЃЌНЋЁїABCбиЙ§DЕФжБЯпелЕўЃЌЪЙЕуAТфдкBCЩЯFДІЃЌВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
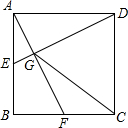 ШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЃЌFЗжБ№ЮЊABЃЌBCЕФжаЕуЃЌAFЃЌDEЯрНЛгкЕуGЃЌСЌНгCGЃЌдђtanЁЯDGC=2ЃЎ
ШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЃЌFЗжБ№ЮЊABЃЌBCЕФжаЕуЃЌAFЃЌDEЯрНЛгкЕуGЃЌСЌНгCGЃЌдђtanЁЯDGC=2ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2$\sqrt{2}$cm | BЃЎ | 4$\sqrt{2}$cm | CЃЎ | 8$\sqrt{2}$cm | DЃЎ | вдЩЯНсТлЖМВЛЖд |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
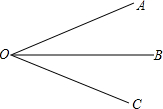 ШчЭМЁЯAOC=60ЁуЃЌOBЪЧЁЯAOCЕФЦНЗжЯпЃЌШєдйАбЁЯAOBЫФЕШЗжЃЌУПвЛЗнЪЧЖрЩйЖШНЧЃЈОЋШЗЕНЗжЃЉЃП
ШчЭМЁЯAOC=60ЁуЃЌOBЪЧЁЯAOCЕФЦНЗжЯпЃЌШєдйАбЁЯAOBЫФЕШЗжЃЌУПвЛЗнЪЧЖрЩйЖШНЧЃЈОЋШЗЕНЗжЃЉЃПВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com