

分析 (1)作辅助线,构建四边形ECFD,证明四边形ECFD是正方形,根据DE∥BC和DF∥AC列比例式得①②式:相加得:$\frac{EC}{AC}+\frac{CF}{BC}$=$\frac{BD+AD}{AB}$=1,根据△ECD是等腰直角三角形得:EC=CF=$\frac{\sqrt{2}}{2}$CD,代入可得结论;
(2)根据AD∥BC∥EF,得比例式:$\frac{EO}{AD}=\frac{EB}{AB}$,$\frac{FO}{AD}=\frac{FC}{CD}$,$\frac{EB}{AB}=\frac{FC}{CD}$,得EO=FO,根据EF∥AD得比例式①和②,同(1)得:相加后化简得结论.
解答  证明:(1)如图1,过D作DE⊥AC于E,DF⊥BC于F,
证明:(1)如图1,过D作DE⊥AC于E,DF⊥BC于F,
∵CD平分∠ACB,
∴ED=FD,
∵∠DEC=∠ECF=∠CFD=90°,
∴四边形ECFD是矩形,
∵ED=FD,
∴四边形ECFD是正方形,
∴EC=CF=$\frac{\sqrt{2}}{2}$CD,
∵DE∥BC,
∴$\frac{EC}{AC}=\frac{BD}{AB}①$,
同理得:$\frac{CF}{BC}=\frac{AD}{AB}②$,
①+②得:$\frac{EC}{AC}+\frac{CF}{BC}$=$\frac{BD+AD}{AB}$=1,
∵EC=CF=$\frac{\sqrt{2}}{2}$CD,
∴$\frac{\frac{\sqrt{2}}{2}CD}{AC}$+$\frac{\frac{\sqrt{2}}{2}CD}{BC}$=1,
∴$\frac{CD}{AC}+\frac{CD}{BC}$=$\sqrt{2}$;
(2)如图2,∵AD∥BC,EF∥BC,
∴AD∥BC∥EF,
∴$\frac{EO}{AD}=\frac{EB}{AB}$,
$\frac{FO}{AD}=\frac{FC}{CD}$,
$\frac{EB}{AB}=\frac{FC}{CD}$,
∴$\frac{EO}{AD}=\frac{FO}{AD}$,
∴EO=FO,
∵EO∥AD,
∴$\frac{EO}{AD}=\frac{BO}{BD}$①,
同理可得:$\frac{FO}{BC}=\frac{OD}{BD}$②,
①+②得:$\frac{EO}{AD}+\frac{FO}{BC}$=$\frac{BO}{BD}+\frac{OD}{BD}$=1,
∵OE=OF=$\frac{1}{2}$EF,
∴$\frac{\frac{1}{2}EF}{AD}+\frac{\frac{1}{2}EF}{BC}$=1,
∴$\frac{EF}{AD}+\frac{EF}{BC}$=2.
点评 本题考查了平行线分线段成比例定理、矩形和正方形的性质和判定,有难度,本题证明的结论是定值问题,因此从平行线分线段成比例定理得比例式入手,运用类比的方法,将所得比例式①和②相加并进一步化简得出结论.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{{8}^{2}}$的平方根是±2 | B. | $\root{3}{(x-1)^{3}}$的立方根是±(x-1) | ||
| C. | $\sqrt{(-3)^{2}}$的立方根是$\root{3}{3}$ | D. | 若$\sqrt{-x}$有意义,则$\sqrt{-x}$≥0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
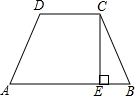 已知在梯形ABCD中,AB∥CD,CE⊥AB,垂足为E,梯形的面积为80,CE=8.
已知在梯形ABCD中,AB∥CD,CE⊥AB,垂足为E,梯形的面积为80,CE=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )| A. | 15cm | B. | 20cm | C. | 25cm | D. | 30cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
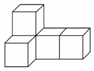 如图,它是由5个完全相同的小正方体搭建的几何体,若将最右边的小正方体拿走,则下列结论正确的是( )
如图,它是由5个完全相同的小正方体搭建的几何体,若将最右边的小正方体拿走,则下列结论正确的是( )| A. | 主视图不变 | B. | 左视图不变 | C. | 俯视图不变 | D. | 三视图都不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 84.5分 | B. | 85分 | C. | 84分 | D. | 83分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com