
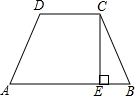
 已知在梯形ABCD中,AB∥CD,CE⊥AB,垂足为E,梯形的面积为80,CE=8.
已知在梯形ABCD中,AB∥CD,CE⊥AB,垂足为E,梯形的面积为80,CE=8.分析 (1)设AB=5a,CD=3a,根据梯形的面积公式,列出方程即可解决问题.
(2)如图作DH⊥AB于H,由Rt△ADH≌Rt△BCE,推出AH=EB=CE÷tan60°=$\frac{8}{\sqrt{3}}$,设CD=HE=x,由题意$\frac{1}{2}$(2x+$\frac{16}{\sqrt{3}}$)•8=80,列方程即可.
解答 解:(1)设AB=5a,CD=3a,
由题意$\frac{1}{2}$•(5a+3a)•8=80,
∴a=$\frac{5}{2}$,
∴AB=$\frac{25}{2}$,CD=$\frac{15}{3}$.
(2)如图作DH⊥AB于H,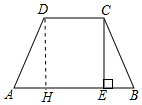
∵CD∥AB,DH⊥AB,CE⊥AB,
∴DH=CE,
在Rt△ADH和Rt△BCE中,
$\left\{\begin{array}{l}{AD=BC}\\{DH=CE}\end{array}\right.$,
∴Rt△ADH≌Rt△BCE,
∴AH=EB=CE÷tan60°=$\frac{8}{\sqrt{3}}$,设CD=HE=x,
由题意$\frac{1}{2}$(2x+$\frac{16}{\sqrt{3}}$)•8=80,
∴x=10-$\frac{8\sqrt{3}}{3}$,
∴AB=10+$\frac{8\sqrt{3}}{3}$,CD=10-$\frac{8\sqrt{3}}{3}$.
点评 本题考查梯形的性质,全等三角形的判定和性质等知识,解题的关键是学会构建方程解决问题,学会添加常用辅助线构造全等三角形,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 3.844×106 | B. | 3.844×107 | C. | 3.844×108 | D. | 3.844×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨眉山 |
| 海拔(m) | 1524 | 1997 | 1873 | 1500 | 3099 |
| A. | 扇形统计图 | B. | 条形统计图 | C. | 折线统计图 | D. | 以上三种都可以 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com