
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).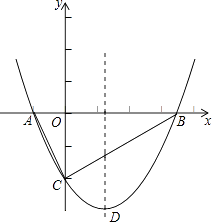
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
【答案】
(1)
解:∵点A(﹣1,0)在抛物线 ![]() 上,
上,
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为 ![]() .
.
∵ ![]() ,
,
∴顶点D的坐标为 ![]() ;
;
(2)
解:△ABC是直角三角形.理由如下:
当x=0时,y=﹣2,
∴C(0,﹣2),则OC=2.
当y=0时, ![]() ,
,
∴x1=﹣1,x2=4,则B(4,0),
∴OA=1,OB=4,
∴AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(3)
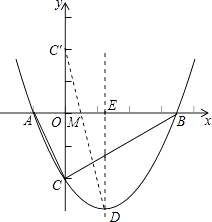
解:作出点C关于x轴的对称点C′,则C'(0,2).
连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,CD一定,当MC+MD的值最小时,△CDM的周长最小.
设直线C′D的解析式为y=ax+b(a≠0),则
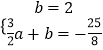 ,
,
解得 ![]() ,
,
∴ ![]() .
.
当y=0时, ![]() ,则
,则 ![]() ,
,
∴ ![]() .
.
【解析】(1)把点A的坐标代入抛物线解析式,列出关于系数b的方程,通过解方程求得b的值;利用配方法把抛物线解析式转化为顶点式方程,根据该解析式直接写出顶点D的坐标;(2)利用点A、B、C的坐标来求线段AB、AC、BC的长度,得到AC2+BC2=AB2 , 则由勾股定理的逆定理推知△ABC是直角三角形;(3)作出点C关于x轴的对称点C′,则C'(0,2).连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,CD一定,当MC+MD的值最小时,△CDM的周长最小.利用待定系数法求得直线C′D的解析式,然后把y=0代入直线方程,求得 ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
A.( ![]() ,1)
,1)
B.(1,﹣ ![]() )
)
C.(2 ![]() ,﹣2)
,﹣2)
D.(2,﹣2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明本学期的数学测验成绩如表所示:
测验 类别 | 平时测验 | 期中 测验 | 期末 测验 | |||
第1次 | 第2此 | 第3次 | 第4次 | |||
成绩 | 80 | 86 | 84 | 90 | 90 | 95 |
(1)求六次测验成绩的众数和中位数;
(2)求小明本学期的数学平时测验的平均成绩;
(3)如果本学期的总评成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照3:3:4的比例计算所得,计算小明本学期学科的总评成绩。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
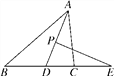
【题目】如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,当P点在线段AD上运动时,∠E与∠B,∠ACB的数量关系为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m. 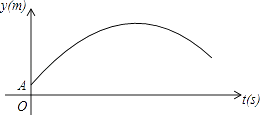
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com