
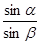 = .
= .
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源:不详 题型:解答题
 的正方形网格中,每个小正方形的边长
的正方形网格中,每个小正方形的边长
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
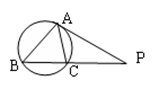
 点,并测得HB=6m.
点,并测得HB=6m.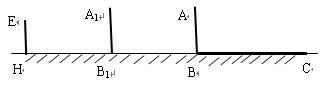
 在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 点出发,他们在岸边跑的速度都是5米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°,请你通过计算说明谁先到达营救地点
点出发,他们在岸边跑的速度都是5米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°,请你通过计算说明谁先到达营救地点 .
.



查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.(24-10 )m )m | B.(24-  m m | C.(24-5 )m )m | D.9m |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com