
分析 根据1<$\sqrt{3}$<2,可得m,n的值,根据代数式求值,可得答案.
解答 解:由1<$\sqrt{3}$<2,得m=3,n=$\frac{\sqrt{3}+1}{\sqrt{3}-1}$-3,
m2-$\sqrt{3}mn+{n}^{2}$=32-3$\sqrt{3}$($\frac{4-2\sqrt{3}}{\sqrt{3}-1}$)+($\frac{4-2\sqrt{3}}{\sqrt{3}-1}$)2
=9-$\frac{12\sqrt{3}-18}{\sqrt{3}-1}$+4-2$\sqrt{3}$
=9-(9-3$\sqrt{3}$)+4-2$\sqrt{3}$
=$\sqrt{3}$+4.
点评 本题考查了估算无理数的大小,利用1<$\sqrt{3}$<2,得出m,n的值是解题关键,注意要分母有理化.


科目:初中数学 来源: 题型:填空题
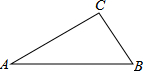 在△ABC中,∠ACB=90°,若∠A=30°,CA=6,则AB的长为,4$\sqrt{3}$,△ABC的面积为6$\sqrt{3}$.
在△ABC中,∠ACB=90°,若∠A=30°,CA=6,则AB的长为,4$\sqrt{3}$,△ABC的面积为6$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
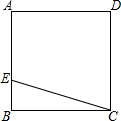 如图,ABCD是一块正方形的场地,小华和小芳在AB边上选定了一点E,测量知EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
如图,ABCD是一块正方形的场地,小华和小芳在AB边上选定了一点E,测量知EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
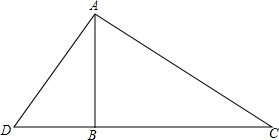 如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长?
如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com