Question

【题目】如图，已知△ABC的面积为24，点D在线段AC上，点F在线段BC的延长线上，且BF=4CF，四边形DCFE是平行四边形，则图中阴影部分的面积为（ ）

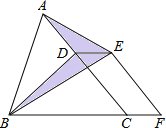
A．3 B．4 C．6 D．8

Answer 1

【答案】D

【解析】

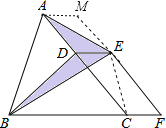
试题分析：连接EC，过A作AM∥BC交FE的延长线于M，求出平行四边形ACFM，根据等底等高的三角形面积相等得出△BDE的面积和△CDE的面积相等，△ADE的面积和△AME的面积相等，推出阴影部分的面积等于平行四边形ACFM的面积的一半，求出CF×hCF的值即可．

解：连接EC，过A作AM∥BC交FE的延长线于M，

∵四边形CDEF是平行四边形，

∴DE∥CF，EF∥CD，

∴AM∥DE∥CF，AC∥FM，

∴四边形ACFM是平行四边形，

∵△BDE边DE上的高和△CDE的边DE上的高相同，

∴△BDE的面积和△CDE的面积相等，

同理△ADE的面积和△AME的面积相等，

即阴影部分的面积等于平行四边形ACFM的面积的一半，是×CF×hCF，

∵△ABC的面积是24，BC=3CF

∴BC×hBC=×3CF×hCF=24，

∴CF×hCF=16，

∴阴影部分的面积是×16=8，

故选：D．