
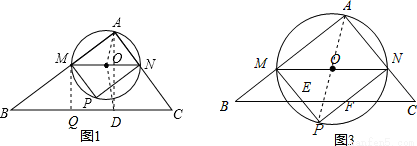
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.

(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
(1)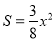 .(0<x<4)(2)x=
.(0<x<4)(2)x=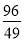 时,⊙O与直线BC相切;(3)y=-
时,⊙O与直线BC相切;(3)y=-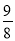 x2+6x-6,当x=
x2+6x-6,当x=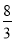 时,y值最大,最大值是2.
时,y值最大,最大值是2.
【解析】
试题分析:(1)由于三角形PMN和AMN的面积相当,那么可通过求三角形AMN的面积来得出三角形PMN的面积,求三角形AMN的面积可根据三角形AMN和ABC相似,根据相似比的平方等于面积比来得出三角形AMN的面积;
(2)当圆O与BC相切时,O到BC的距离就是MN的一半,那么关键是求出MN的表达式,可根据三角形AMN和三角形ABC相似,得出MN的表达式,也就求出了O到BC的距离的表达式,如果过M作MQ⊥BC于Q,那么MQ就是O到BC的距离,然后在直角三角形BMQ中,用∠B的正弦函数以及BM的表达式表示出MQ,然后让这两表示MQ的含x的表达式相等,即可求出x的值;
(3)要求重合部分的面积首先看P点在三角形ABC内部还是外面,因此可先得出这两种情况的分界线即当P落到BC上时,x的取值,那么P落点BC上时,MN就是三角形ABC的中位线,此时AM=2,因此可分两种情况进行讨论:
①当0<x≤2时,此时重合部分的面积就是三角形PMN的面积,三角形PMN的面积(1)中已经求出,即可的x,y的函数关系式.②当2<x<4时,如果设PM,PN交BC于E,F,那么重合部分就是四边形MEFN,可通过三角形PMN的面积-三角形PEF的面积来求重合部分的面积.不难得出PN=AM=x,而四边形BMNF又是个平行四边形,可得出FN=BM,也就有了FN的表达式,就可以求出PF的表达式,然后参照(1)的方法可求出三角形PEF的面积,即可求出四边形MEFN的面积,也就得出了y,x的函数关系式.然后根据两种情况得出的函数的性质,以及对应的自变量的取值范围求出y的最大值即可.
试题解析:(1)∵MN∥BC,
∴∠AMN=∠B,∠ANM=∠C.
∴△AMN∽△ABC.
∴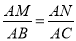 ,
,
即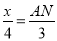 ;
;
∴AN=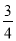 x;
x;
∴S=S△MNP=S△AMN=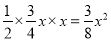 .(0<x<4)
.(0<x<4)
(2)如图2,设直线BC与⊙O相切于点D,连接AO,OD,则AO=OD=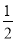 MN.
MN.
在Rt△ABC中,BC=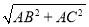 =5;
=5;
由(1)知△AMN∽△ABC,
∴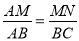 ,
,
即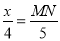 ,
,
∴MN=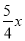
∴OD=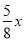 ,
,
过M点作MQ⊥BC于Q,则MQ=OD=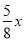 ,
,
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA,
∴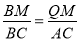 ,
,
∴BM= ,AB=BM+MA=
,AB=BM+MA=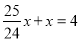
∴x=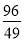 ,
,
∴当x=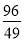 时,⊙O与直线BC相切;
时,⊙O与直线BC相切;
(3)随点M的运动,当P点落在直线BC上时,连接AP,则O点为AP的中点.
∵MN∥BC,
∴∠AMN=∠B,∠AOM=∠APB,
∴△AMO∽△ABP,
∴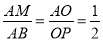 ,
,
∵AM=MB=2,
故以下分两种情况讨论:
①当0<x≤2时,y=S△PMN=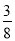 x2,
x2,
∴当x=2时,y最大=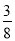 ×4=
×4=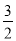 ,
,
②当2<x<4时,设PM,PN分别交BC于E,F,
∵四边形AMPN是矩形,
∴PN∥AM,PN=AM=x,
又∵MN∥BC,
∴四边形MBFN是平行四边形;
∴FN=BM=4-x,
∴PF=x-(4-x)=2x-4,
又∵△PEF∽△ACB,
∴(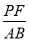 )2=
)2=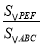 ,
,
∴S△PEF=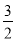 (x-2)2;
(x-2)2;
y=S△MNP-S△PEF=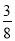 x2-
x2-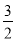 (x-2)2=-
(x-2)2=-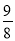 x2+6x-6,
x2+6x-6,
当2<x<4时,y=-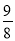 x2+6x-6=-
x2+6x-6=-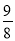 (x-
(x-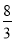 )2+2,
)2+2,
∴当x=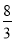 时,满足2<x<4,y最大=2.
时,满足2<x<4,y最大=2.
综上所述,当x=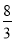 时,y值最大,最大值是2.
时,y值最大,最大值是2.
考点:二次函数综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2015届内蒙古满洲里市八年级下学期期末考试数学试卷(解析版) 题型:选择题
如图,在三角形纸片ABC中,AC=6,∠A=30º,∠C=90º,将∠A沿DE折叠,使点A与点B重合,则折痕DE的长为( )
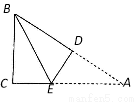
A.1 B.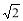 C.
C.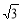 D.2
D.2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上数学期末模拟数学试卷(解析版) 题型:选择题
已知点A(-2 ,y1),(-1 ,y2),(3 ,y3)都在反比例函数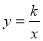 (k>0)的图象上,则( )
(k>0)的图象上,则( )
A.y1<y2<y3 B.y3<y2<y1 C.y3 <y1<y2 D.y2<y1<y3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省泰安市毕业生学业水平模拟二数学试卷(解析版) 题型:填空题
“上升数”是一个数中右边数字比左边数字大的自然数(如:34,568,2469等).任取一个两位数,是 “上升数”的概率是
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省泰安市毕业生学业水平模拟二数学试卷(解析版) 题型:选择题
某电子元件厂准备生产4600个电子元件,甲车间独立生产了一半后,由于要尽快投入市场,乙车间也加入该电子元件的生产,若乙车间每天生产的电子元件是甲车间的1.3倍,结果用33天完成任务,问甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可得方程为( )
A.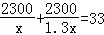
B.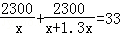
C.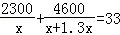
D.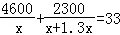
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古化德县第三中学九年级上学期期末测试数学试卷(解析版) 题型:解答题
如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.
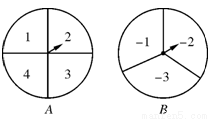
(1)用画树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com