
【题目】如图,已知四边形ABCD是正方形,△AEF是等边三角形,E,F分别位于DC边和BC边上.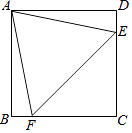
(1)求∠DAE的度数;
(2)若正方形ABCD的边长为1,求等边三角形AEF的面积;
(3)将△AEF绕着点E逆时针旋转m(0<m<180)度,使得点A落在正方形ABCD的边上,求m的值.
【答案】
(1)解:∵四边形ABCD是正方形,
∴AB=AD,AF=AE,∠B=∠D=90°,
在Rt△ABF与Rt△ADE, ![]() ,
,
∴Rt△ABF≌Rt△ADE,
∴∠DAE=∠BAF
又∠DAE+∠BAF=∠BAD﹣∠EAF=90°﹣60°=30°
∴∠DAE=15°;
(2)解:设BF=x,由(1)可知DE=BF=x,则CF=CE=1﹣x
∴AB2+BF2=AF2,CF2+CE2=EF2,AF=EF,
即:12+x2=2(1﹣x)2
∴x1=2+ ![]() ,x2=2
,x2=2 ![]() ,
,
∵0<x<1,
∴x1=2+ ![]() (舍去),x=2
(舍去),x=2 ![]() ,
,
∴S△AEF=S四边形ABCD﹣2S△ABF﹣S△EFC=12﹣2× ![]() 1×(2﹣
1×(2﹣ ![]() )﹣
)﹣ ![]() (
( ![]() ﹣1)2=2
﹣1)2=2 ![]() ﹣3;
﹣3;
(3)解:依题意,点A可落在AB边上或BC边上.
①当点A落在AB边上时,设此时点A的对应点为M,则EA=EM,
∵∠EAB=75°,
∴∠AME=75°,
∴m=∠AEM=180°﹣75°﹣75°=30°,
②当点A落在边BC上时,
∵EA=EF,点A旋转后与点F重合,
∴m=∠AEF=60°,
综上,m=30°或m=60°.
【解析】(1)由正方形性质得AB=AD,AF=AE,∠B=∠D=90°,再根据直角三角形的判定得Rt△ABF≌Rt△ADE(HL),由全等三角形的性质得∠DAE=∠BAF,由等边三角形和正方形的性质得∠DAE的度数.
(2)设BF=x,由(1)知DE=BF=x,则CF=CE=1﹣x,由勾股定理得AB2+BF2=AF2,CF2+CE2=EF2,AF=EF,即12+x2=2(1﹣x)2(0<x<1),
求出x=2 ![]() ,再由S△AEF=S四边形ABCD﹣2S△ABF﹣S△EFC求出即可.
,再由S△AEF=S四边形ABCD﹣2S△ABF﹣S△EFC求出即可.
(3)依题分两种情况来分析:①当点A落在AB边上时,设此时点A的对应点为M,则EA=EM;②当点A落在边BC上时;根据旋转的性质和三角形内角和定理即可求出答案.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
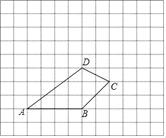
(1)请画出将四边形ABCD向上平移5个单位长度,再向左平移2个单位长度后所得的四边形A′B′C′D′.
(2)求线段AB扫过的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
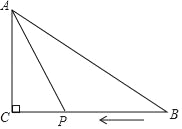
【题目】如图,在三角形ABC中,∠C=90°,AC=6cm,BC=10cm,点P从B点开始向C点运动速度是每秒1cm,设运动时间是t秒,
(1)用含t的代数式来表示三角形ACP的面积.
(2)当三角形ACP的面积是三角形ABC的面积的一半时,求t的值,并指出此时点P在BC上的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
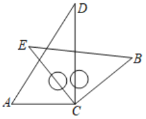
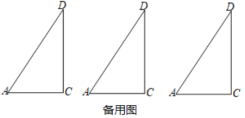
【题目】将一副三角板中的两块直角三角尺的直角顶点![]() 按如图所示的方式叠放在一起(其中
按如图所示的方式叠放在一起(其中![]() ,
,![]() ,
,![]() ),固定三角板
),固定三角板![]() ,另一三角板
,另一三角板![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 顺时针旋转,设旋转的角度为
顺时针旋转,设旋转的角度为![]() .
.
(1)当![]() 时;
时;
①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,求
,求![]() 的度数;
的度数;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() 时,这两块三角尺是否存在一组边互相垂直?若存在,请直接写出
时,这两块三角尺是否存在一组边互相垂直?若存在,请直接写出![]() 所有可能的值,并指出哪两边互相垂直(不必说明理由);若不存在,请说明理由.
所有可能的值,并指出哪两边互相垂直(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是( )

A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
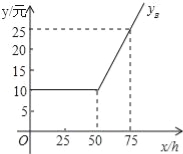
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
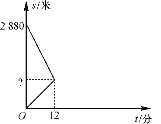
【题目】五一假期过后,小明到校后发现忘记带数学课本,一看手表,离上课还有20分钟,他立刻步行返回家中取书,同时,他的父亲也发现小明忘记带数学课本,带上课本立刻以小明步行速度的2倍骑车赶往学校.父子在途中相遇,小明拿到课本后马上按原速步行返回学校,到校后发现迟到了4分钟.如图是父子俩离学校的路程s(米)与所用时间t(分)之间的函数关系,请结合图像,回答下列问题:
(1)两人相遇处离学校的距离是多少米?
(2)试求小明的父亲在赶往学校的过程中,路程s与时间t之间的函数表达式;
(3)假如小明父子相遇拿到课本后,改由他的父亲骑车搭他到学校,他会迟到吗?如果会,迟到几分钟;如果不会,能提前几分钟到校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知2x﹣1的平方根是±6,2x+y﹣1的算术平方根是5,求2x﹣3y+11的立方根.
(2)已知x是1的平方根,求代数式(x2017﹣1)(x2018﹣712)(x2019+1)(x2020+712)+1000x的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com