
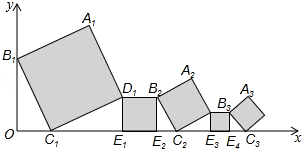
分析 根据勾股定理可得正方形A1B1C1D1的边长为$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,根据相似三角形的性质可得后面正方形的边长依次是前面正方形边长的$\frac{1}{2}$,依次得到第2015个正方形和第2015个正方形的边长,进一步得到点A2015到x轴的距离.
解答 解:如图,∵点C1、E1、E2、C2、E3、E4、C3在x轴上,B1C1∥B2C2∥B3C3,
∴△B1OC1∽△B2E2C2∽B3E4C3…,△B1OC1≌△C1E1D1,…,
∴B2E2=1,B3E4=$\frac{1}{2}$,B4E6=$\frac{1}{4}$,B5E8=$\frac{1}{8}$…,
∴B2015E4017=$\frac{1}{{2}^{2013}}$,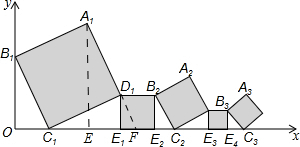
作A1E⊥x轴,延长A1D1交x轴于F,
则△C1D1F∽△C1D1E1,
∴$\frac{{D}_{1}F}{{D}_{1}{E}_{1}}=\frac{{C}_{1}{D}_{1}}{{C}_{1}{E}_{1}}$,
在Rt△OB1C1中,OB1=2,OC1=1,
正方形A1B1C1D1的边长为$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,
∴D1F=$\frac{\sqrt{5}}{2}$,
∴A1F=$\frac{3\sqrt{5}}{2}$,
∵A1E∥D1E1,
∴$\frac{{A}_{1}E}{{D}_{1}{E}_{1}}=\frac{{A}_{1}F}{{D}_{1}F}$,
∴A1E=3,
∴$\frac{{A}_{1}E}{{B}_{1}O}=\frac{3}{2}$,
∴点A2015到x轴的距离是$\frac{1}{{2}^{2013}}×\frac{3}{2}=\frac{3}{{2}^{2014}}$,
故答案为$\frac{3}{{2}^{2014}}$
点评 此题主要考查了正方形的性质以及解直角三角形的知识,得出正方形各边长是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
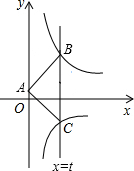 如图,直线x=t(t>0)与反比例函数y=$\frac{k}{x}$(x>0)、y=$\frac{-1}{x}$(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
如图,直线x=t(t>0)与反比例函数y=$\frac{k}{x}$(x>0)、y=$\frac{-1}{x}$(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.12348×104次 | B. | 0.512348×105次 | C. | 5.12348×108次 | D. | 5.12348×109次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).
某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com