
【题目】如图,正方形ABCD中,AB=3cm,以B为圆心,1cm为半径画圆,点P是⊙B上一个动点,连接AP,并将AP绕点A逆时针旋转90°至AP',连接BP',在点P移动的过程中,BP'长度的取值范围是_____cm.

【答案】(3![]() -1)cm≤BP≤(3
-1)cm≤BP≤(3![]() +1).
+1).
【解析】
通过画图发现,点P′的运动路线为以D为圆心,以1为半径的圆,可知:当P′在对角线BD上时,BP′最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出BP′的长.
如图,当P′在对角线BD上时,BP′最小;当P′在对角线BD的延长线上时,BP′最大.
连接BP,
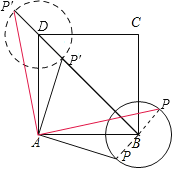
①当P′在对角线BD上时,
由旋转得:AP=AP′,∠PAP′=90°,
∴∠PAB+∠BAP′=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAP′+∠DAP′=90°,
∴∠PAB=∠DAP′,
∴△PAB≌△P′AD,
∴P′D=PB=1,
在Rt△ABD中,∵AB=AD=3,
由勾股定理得:BD=![]() =3
=3![]() ,
,
∴BP′=BD-P′D=3![]() -1,
-1,
即BP′长度的最小值为(3![]() -1)cm.
-1)cm.
②当P′在对角线BD的延长线上时,
同理可得BD=![]() =3
=3![]() ,
,
∴BP′=BD+P′D=3![]() +1,
+1,
即BP′长度的最大值为(3![]() +1)cm.
+1)cm.
∴BP'长度的取值范围是(3![]() -1)cm≤BP≤(3
-1)cm≤BP≤(3![]() +1)cm
+1)cm
故答案为:(3![]() -1)cm≤BP≤(3
-1)cm≤BP≤(3![]() +1).
+1).


科目:初中数学 来源: 题型:
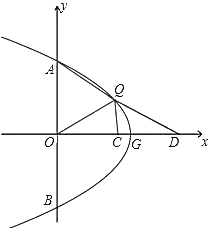
【题目】点P为拋物线![]() 为常数,
为常数,![]() )上任意一点,将抛物线绕顶点G逆时针旋转90°后得到的图象与
)上任意一点,将抛物线绕顶点G逆时针旋转90°后得到的图象与![]() 轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
(1)抛物线![]() 的对称轴是直线________,当m=2时,点P的横坐标为4时,点Q的坐标为_________;
的对称轴是直线________,当m=2时,点P的横坐标为4时,点Q的坐标为_________;
(2)设点Q![]() 请你用含m,
请你用含m,![]() 的代数式表示
的代数式表示![]() 则
则![]() ________;
________;
(3)如图,点Q在第一象限,点D在![]() 轴的正半轴上,点C为OD的中点,QO平分∠AQC,当AQ=2QC,QD=
轴的正半轴上,点C为OD的中点,QO平分∠AQC,当AQ=2QC,QD=![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P(m,4)在反比例函数y=﹣![]() 的图象上,正比例函数的图象经过点P和点Q(6,n).
的图象上,正比例函数的图象经过点P和点Q(6,n).
(1)求正比例函数的解析式;
(2)求P、Q两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
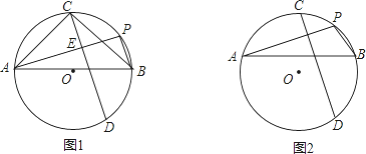
【题目】(1)如图1,PA、PB是⊙O的两条弦,AB为直径,C为![]() 的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
(2)如图2,PA、PB是⊙O的两条弦,AB为弦,C为劣弧![]() 的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
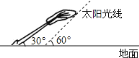
【题目】如图,太阳光线与地面成![]() 角,一棵倾斜的大树与地面成
角,一棵倾斜的大树与地面成![]() 角,这时测得大树在地面上的影长约为
角,这时测得大树在地面上的影长约为![]() ,则大树的长约为________
,则大树的长约为________![]() (保留两个有效数字,下列数据供选用:
(保留两个有效数字,下列数据供选用:![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
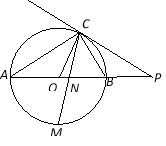
(1)求证:PC是⊙O的切线;
(2)求证:BC=AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com