练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

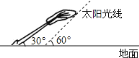
    【题目】如图，太阳光线与地面成角，一棵倾斜的大树与地面成角，这时测得大树在地面上的影长约为，则大树的长约为________（保留两个有效数字，下列数据供选用：，）．

    【答案】

    【解析】

    画出示意图，过树梢向地面引垂线，利用60°的正弦值求出CD后，进而利用30°的正弦值即可求得AC长.

    解：∵太阳光线与地面成60°角，一棵倾斜的大树与地面成30°角，作∠CBD=60°，则C在地面的影子是点B，即AB是大树在地面的影长，

    ∵∠CAB=30°，∠CBD=60°，

    ∴∠ACB=30°，

    ∴∠CAB=∠ACB，

    ∴BC=AB=10.

    作CD⊥AB于点D，

    ∴sin∠CBD=sin60°=，

    ∴CD=BC×sin∠CBD=10×.

    在Rt△ACD中，∠CAD=30°，

    ∴AC=2CD=2×≈17(m).

    故答案为：17.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

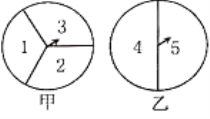
    【题目】如图，甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形．小夏和小秋利用它们来做决定获胜与否的游戏．规定小夏转甲盘一次、小秋转乙盘一次为一次游戏（当指针指在边界线上时视为无效，重转）.

    （1）小夏说：“如果两个指针所指区域内的数之和为6或7，则我获胜；否则你获胜”.按小夏设计的规则，请你写出两人获胜的可能性分别是多少?

    （2）请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则，并用一种合适的方法(例如：树状图，列表)说明其公平性.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将号码分别为1，2，3，…，9的九个小球放入一个袋中，这些小球仅号码不同，其余完全相同，甲从袋中摸出一个球，号码为a，放回后乙再摸出一个球，号码为b，则使不等式成立的事件发生的概率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有3，4，5，x，甲乙两人每次同时从袋中各随机摸出1个小球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复试验，试验数据如图：

    解答下列问题：

    （1）如果试验继续进行下去，根据上表数据，出现“和为8”的频率将稳定在它的概率附近，估计出现“和为8”的概率是 .

    （2）如果摸出的这两个小球上的数字之和为9的概率是，那么x的值可以取7吗？请用列表法或画树状图法说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD中，AB＝3cm，以B为圆心，1cm为半径画圆，点P是⊙B上一个动点，连接AP，并将AP绕点A逆时针旋转90°至AP'，连接BP'，在点P移动的过程中，BP'长度的取值范围是_____cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：

    材料1、若一元二次方程ax2+bx+c=0（a≠0）的两根为x1，x2，则x1+x2=，x1x2=．

    材料2、已知实数m、n满足m2﹣m﹣1=0，n2﹣n﹣1=0，且m≠n，求的值．

    解：由题知m、n是方程x2﹣x﹣1=0的两个不相等的实数根，根据材料1得

    m+n=1，mn=﹣1

    ∴

    根据上述材料解决下面问题；

    （1）一元二次方程2x2+3x﹣1=0的两根为x1、x2，则x1+x2=　 　，x1x2=　 　．

    （2）已知实数m、n满足2m2﹣2m﹣1=0，2n2﹣2n﹣1=0，且m≠n，求m2n+mn2的值．

    （3）已知实数p、q满足p2=3p+2，2q2=3q+1，且p≠2q，求p2+4q2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

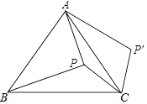
    【题目】如图，点P在等边△ABC的内部，且PC=6，PA=8，PB=10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，则sin∠PAP'的值为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是边长为1的正方形，点E在AD边上运动，且不与点A和点D重合，连结CE，过点C作CF⊥CE交AB的延长线于点F，EF交BC于点G．

    （1）求证：△CDE≌△CBF；

    （2）当DE=时，求CG的长；

    （3）连结AG，在点E运动过程中，四边形CEAG能否为平行四边形？若能，求出此时DE的长；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB＝90°，∠A＝30°，将△ABC绕C点按逆时针方向旋转α角（0°＜α＜90°）得到△DEC，设CD交AB于F，连接AD，△ADF是等腰三角形旋转角α度数为（　　）

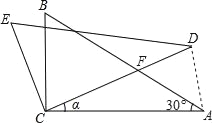
    A. 20° B. 40° C. 20°或40° D. 60°

    查看答案和解析>>

    同步练习册答案