
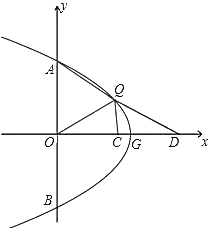
����Ŀ����PΪ������![]() Ϊ������
Ϊ������![]() ��������һ�㣬���������ƶ���G��ʱ����ת90���õ���ͼ����
��������һ�㣬���������ƶ���G��ʱ����ת90���õ���ͼ����![]() �ύ��A��B���㣨��A�ڵ�B���Ϸ�������QΪ��P��ת��Ķ�Ӧ�㣮
�ύ��A��B���㣨��A�ڵ�B���Ϸ�������QΪ��P��ת��Ķ�Ӧ�㣮
��1��������![]() �ĶԳ�����ֱ��________����m=2ʱ����P�ĺ�����Ϊ4ʱ����Q������Ϊ_________��
�ĶԳ�����ֱ��________����m=2ʱ����P�ĺ�����Ϊ4ʱ����Q������Ϊ_________��
��2�����Q![]() �����ú�m��
�����ú�m��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��![]() ________��
________��
��3����ͼ����Q�ڵ�һ���ޣ���D��![]() ����������ϣ���CΪOD���е㣬QOƽ�֡�AQC����AQ=2QC��QD=
����������ϣ���CΪOD���е㣬QOƽ�֡�AQC����AQ=2QC��QD=![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
���𰸡���1��x=m��Q��-2,2������2��a=m-![]() ����3��m=1.
����3��m=1.
��������
��1���䷽���ɵó������ߵĶԳ���������m��ֵȷ����ԭ�����ߵĽ���ʽ�����������P��G����������P��PE��x����E����Q��QF��x����F��������ת������֪����GQF�ա�PGE����QF��GE��PE��GF���ɾݴ���õ�Q��������
��2����֪Q�����������ɵõ�QF��FG�ij������գ�1���ķ����������P��������Ȼ�����ԭ�����ߵĽ���ʽ���������a��b��m�Ĺ�ϵʽ��
��3���ӳ�QC��E��ʹ��QC��CE����ôAQ��QE����֤��QCD�ա�ECO����ôQD��OE��m����AQ��QE����QOƽ�֡�AQC����֤�á�AQO�ա�EQO����OA��OE��m����A������Ϊ��0��m����Ȼ��A��������루2���Ĺ�ϵʽ�����������m��ֵ��
��1��![]() =
=![]() ���Գ���Ϊֱ��x=m��
���Գ���Ϊֱ��x=m��
��m��2ʱ��y����x��2��2����G��2��0����
�ߵ�P�ĺ�����Ϊ4����P�������������ཫx��4���������߽���ʽ����y����4��2��2��4����P��4��4������ͼ������QG��PG������Q��QF��x����F������P��PE��x����E�����������ɵ�����GQF�ա�PGE����FQ��EG��2��FG��EP��4����FO��2����Q����2��2����

��2����֪Q��a��b������GE��QF��b��FG��m��a��
�ɣ�1��֪��PE��FG��m��a��GE��QF��b����P��m+b��m��a��������ԭ�����ߵĽ���ʽ��������m��a����m+b��2��2m��m+b��+m2��m��a��m2+b2+2mb��2m2��2mb+m2��a��m��b2�����ú�m��b�Ĵ���ʽ��ʾa��a��m��b2��
��3����ͼ���ӳ�QC����E��ʹCE��CQ������OE��
��CΪOD�е�����OC��CD��
�ߡ�ECO����QCD�����ECO�ա�QCD����OE��DQ��m��
��AQ��2QC����AQ��QE��
��QOƽ�֡�AQC�����1����2�����AQO�ա�EQO����AO��EO��m����A��0��m����
��A��0��m������ͼ��������0��m��m2����m1��1��m2��0���ᣩ����m��1��


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������飬�ڵ�ʮ����ȫ���˴����ȫ���ȫ��������������������ע�ȷdz��ߣ���ҹ�ע�������ǹ�ע���ȵ㻰��ֱ��У����ѡ������������������������������࣬�ҹ�ע�����ȵ�����������������ռ�ٷֱ���ͼl��ʾ����ע�������ȵ���������������IJ���������ͳ����ͼ2��ʾ�������ͼ����Ϣ����������⣮

(1)���ͼl�й�ע���������������������ռ�ٷֱ�x��ֵ������ͼ2�еIJ�����������ͳ��ͼ����������
(2)Ϊ������̽�������������棬����������ɶ���5����������ס��ҡ������������������˷�̸����һ�η�̸ֻѡ2���������������б�������״ͼ�ķ��������һ����ѡ����ǡ���Ǽ��ҵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D����O��ֱ��AB���ӳ����ϣ���C����O�ϣ�AC��CD����D��30�㣬
��1�����ж�CD�Ƿ���O�����ߣ���˵�����ɣ�
��2������O�İ뾶Ϊ6����AC�ij����������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ֱ��������2��1����3����4�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ���������ȡһ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm�����������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊn��
��1���뻭����״ͼ��д����m��n�����п��ܵĽ����
��2������ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ����һ������������������ε���������Ϊ��A��1��1����B����3��1����C����3����1��
��1������ABC�����Բ��Բ��ΪP�����P������Ϊ_____��
��2����ͼ��ʾ����11��8������ͼ����������ԭ��O��Ϊλ������������ABC�����Ʊ�2��1�Ŵ���A��B��C�Ķ�Ӧ��ֱ�ΪA�䡢B�䡢C�䣬�õ���A��B��C�䣬��ͼ�л�����A��B��C�䣻������A��B��C����x�᷽��ƽ������ƽ��_____��λ��������ʹ��B��C�����ڵ�ֱ������P������
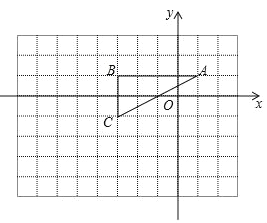
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ת�̱��ֳ�3�������ȵ����Ρ���ת�̱��ֳ�2�������ȵ����Σ�С�ĺ�С��������������������ʤ������Ϸ���涨С��ת����һ�Ρ�С��ת����һ��Ϊһ����Ϸ����ָ��ָ�ڱ߽�����ʱ��Ϊ��Ч����ת��.
��1��С��˵�����������ָ����ָ�����ڵ���֮��Ϊ6��7�����һ�ʤ���������ʤ��.��С����ƵĹ�������д�����˻�ʤ�Ŀ����Էֱ��Ƕ���?
��2�������С�ĺ�С�����������Ϸ���һ�ֹ�ƽ����Ϸ������һ�ֺ��ʵķ���(���磺��״ͼ���б�)˵���乫ƽ��.
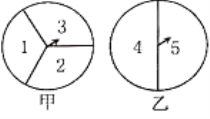
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������ͼ1��2,�ı���![]() ��,��֪
��,��֪![]() ��
��![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��
��1������ͼ 1,��![]() ��
��![]() ����ֱ�ǣ���
����ֱ�ǣ���![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��
��![]() ��ʹ
��ʹ![]() ��
��![]() �غϣ�����֤��
�غϣ�����֤��![]() ����д���������̣�
����д���������̣�
����ͼ 2����![]() ��
��![]() ������ֱ�ǣ���
������ֱ�ǣ���![]() ��
��![]() ����������ϵ_______ʱ������
����������ϵ_______ʱ������![]() ;
;
��2����չ����ͼ3,��![]() �У�
�У�![]() ,
,![]() ����
����![]() ��
��![]() ���ڱ�
���ڱ�![]() ��,��
��,��![]() ����
����![]() ����
����![]() �ij���
�ij���
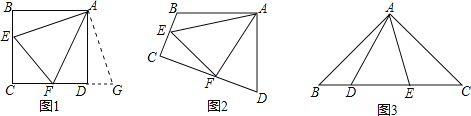
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ��0��2������3��2������2��3����
��1������ͼ�л�����ABC����ƽ��3����λ�����A��B��C�䣻
��2����һ�����κ�����ͼ����1���С�A��B��C�����������㣬��˶��κ����Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD����AB��3cm����BΪԲ����1cmΪ�뾶��Բ����P����B��һ������������AP������AP�Ƶ�A��ʱ����ת90����AP'������BP'���ڵ�P�ƶ��Ĺ�������BP'���ȵ�ȡֵ��Χ��_____cm��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com